Корни многочлена. Основная теорема алгебры.
Если задан f(x) = a0xn+a1xn-1+…+an-1x+an И если, f(x) при некотором с равно нулю, то с наз-ся корнем многочлена и яв-ся решением уравнения f(x)=0 Если f(x) будем делить на многочлен первой степени, то остаток будет многочленом первой степени, если будем делить на ноль - многочленом нулевой степени. Остаток от деления многочлена f(x) на линейный множитель х-с равен значению f(c). F(x) =(x-c)q(x)+r f(c)=r. число с на-ся корнем многочлена уравнения f(x), если f(x) (х-с). Пусть с -корень г(х).Если с яв-ся корнем, то мы получаем, что при подстановке (х-с)=0 то F(x)=(x-c)q(x)+r=0; r=0; f(x)=(x-c)q(x); f(x) (ax+b)—>f(x) (x-(- F(x)=(x-c)q(x)+r (2); f(x) =b 0xn-1+b1xn-2+…+bn-1 (3) Будем сравнивать коэффициенты при равных степенях: a0=b0; a1=b1-cb0; a2=b2-cb1; b0=a0;b1=a1+cb0; bk=ak+cbk-1; k=1,2,…,n-1;an=r-cbn-1;r=an+cbn-1 Теорема: всякий многочлен с любыми числовыми коэффициентами, степень к-ого не меньше 1имеет хотя бы один корень, в общем случае комплексный α1-корень; f(x)=(x- α1)φ(x); f(x)=(x- α1)(x- α2) φ(x); f(x)=(x- α1)(x- α2) (x- α3)… (x- αn) f(x) степени n≥1 с любыми числовыми коэфф. uмеет n корней, если каждый корень имеет столько раз какова его кратность. Формула Виета. f(x) = a0xn+a1xn-1+…+an-1x+an =(x- α1)(x- α2) (x- α3)… (x- αn); α1= - (α1 + α2+…+ αn); α2= α1 α2+…+ αn-1 αn; αn= (-1)n(α1 α2+…+ αn); x3+px2+qx+r=0, x1+x2+x3=-p; x1x2+x2x3+x3x1=q;x1x2x3= - r.
37. Матрица. Понятие матрицы. Матрицей называется прямоугольная таблица из чисел, содержащая некоторое количество m строк и некоторое количество n столбцов. Числа m и n называются порядками матрицы. В случае, если m=n, матрица называется квадратной, а число m=n – ее порядком. Для краткого обозначения матрицы используется либо одна большая латинская буква, например А, либо символ В случае квадратной матрицы вводятся понятия главной и побочной диагонали. Главной диагональю матрицы называется диагональ a11 a22…ann, идущая из левого верхнего угла этой матрицы в правый нижний ее угол. Побочной диагональю той же матрицы называется диагональ ап1а(п-1)2…, идущая из левого нижнего угла в правый верхний угол. Основные операции над матрицами и их свойства. Две матрицы равны, если эти матрицы имеют одинаковые порядки и все их соответствующие элементы совпадают. a) Сложение матриц. Суммой двух матриц b) Умножение матриц на число. Произведением матрицы Для обозначения произведения матрицы на число используется запись или Свойства операции умножения: 1) сочетательным свойством относительно числового множителя: 2) распределительным свойством относительно суммы матриц: 3) распределительным свойством относительно суммы чисел: Замечание. Разностью двух матриц А и В одинаковых порядков т и п естественно назвать такую матрицу С тех же порядков т и п, которая в сумме с матрицей В дает матрицу А. Для обозначения разности двух матриц используется естественная запись: С = А — В. c) Перемножение матриц. Произведением матрицы Это правило можно сформулировать и словесно: элемент 1) сочетательное свойство: (АВ)С = А(ВС); 2) распределительное относительно суммы матриц свойство: (А + В)С = АС + ВС или А(В + С) = АВ + АС. 38. Линейная зависимость/независимость столбцов/строк. Определение. Строки (столбцы) матрицы называются линейно зависимыми, если существует их линейная комбинация, не все коэффициенты в которой равны 0, равная нулевой строке (столбцу). В противном случае строки (столбцы) называются линейно независимыми. Замечание. Можно доказать, что необходимым и достаточным условием линейной зависимости строк матрицы является то, что одна из них является линейной комбинацией остальных. Теорема. Строки и столбцы матрицы, элементы которых входят в базисный минор, линейно независимы. Любая строка (столбец) матрицы является линейной комбинацией этих строк (столбцов). Доказательство (для строк). 1. Если бы базисные строки были линейно зависимыми, то с помощью эквивалентных преобразований из них можно было бы получить нулевую строку, что противоречит условию, что базисный минор не равен 0.2. Строка, входящая в базисный минор, является линейной комбинацией его строк, в которой коэффициент при данной строке равен 1, а остальные коэффициенты равны 0. Докажем это свойство для строки, не входящей в базисный минор. Добавим к базисному минору эту строку (пусть ее номер – k) и любой столбец матрицы (пусть его номер – j). Затем разложим полученный определитель, равный 0 (так как его порядок больше ранга матрицы) по j-му столбцу:
|

 )) обозначим-
)) обозначим-  = с. F(x) (х-с). To есть фактически задача разыскания корней многочлена равносильна нахождению линейных множителей. Теорема Горнера:
= с. F(x) (х-с). To есть фактически задача разыскания корней многочлена равносильна нахождению линейных множителей. Теорема Горнера: . Числа
. Числа  , входящие в состав данной матрицы, называются ее элементами. В записи
, входящие в состав данной матрицы, называются ее элементами. В записи 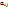 первый индекс i означает номер строки, а второй индекс j-номер столбца.
первый индекс i означает номер строки, а второй индекс j-номер столбца.
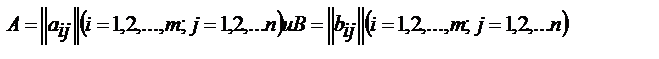 одних и тех же порядков m и n называется матрица
одних и тех же порядков m и n называется матрица  тех же порядков m и n, элементы
тех же порядков m и n, элементы 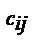 которой равны
которой равны  . Для обозначения суммы двух матриц используется запись С=А+В. Свойства операции сложения: 1) переместительное свойство А+В=В+А; 2) сочетательное свойство: (А+В)+С=А+(В+С).
. Для обозначения суммы двух матриц используется запись С=А+В. Свойства операции сложения: 1) переместительное свойство А+В=В+А; 2) сочетательное свойство: (А+В)+С=А+(В+С). на вещественное число
на вещественное число 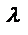 называется матрица
называется матрица  , элементы
, элементы 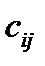 которой равны
которой равны 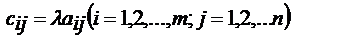
 . Операция составления произведения матрицы на число называется умножением матрицы на это число.
. Операция составления произведения матрицы на число называется умножением матрицы на это число.


 , имеющей порядки, соответственно равные m и n, на матрицу
, имеющей порядки, соответственно равные m и n, на матрицу  , имеющие порядки, соответственно равные n и p, называется матрица
, имеющие порядки, соответственно равные n и p, называется матрица 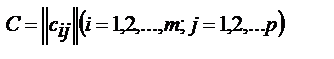 , имеющая порядки соответственно равные m и p, и элементы
, имеющая порядки соответственно равные m и p, и элементы 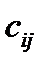 , определяемые формулой
, определяемые формулой 
 , стоящий на пересечении i-й строки и j-го столбца матрицы С = А * В, равен сумме попарных произведений соответствующих элементов i-й строки матрицы А и j-го столбца матрицы В. Для обозначения произведения матрицы А на матрицу В используют запись С = А*В. Операция составления произведения матрицы А на матрицу В называется перемножением этих матриц. Из сформулированного выше определения вытекает, что матрицу А можно умножить не на всякую матрицу В: необходимо, чтобы число столбцов матрицы А было равно числу строк матрицы В. Свойства произведения матриц:
, стоящий на пересечении i-й строки и j-го столбца матрицы С = А * В, равен сумме попарных произведений соответствующих элементов i-й строки матрицы А и j-го столбца матрицы В. Для обозначения произведения матрицы А на матрицу В используют запись С = А*В. Операция составления произведения матрицы А на матрицу В называется перемножением этих матриц. Из сформулированного выше определения вытекает, что матрицу А можно умножить не на всякую матрицу В: необходимо, чтобы число столбцов матрицы А было равно числу строк матрицы В. Свойства произведения матриц: Поскольку
Поскольку 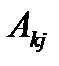 является базисным минором,
является базисным минором, 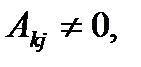 поэтому, разделив полученное равенство на
поэтому, разделив полученное равенство на 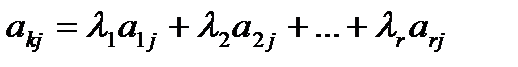 для всех j=1,2,…,n, где
для всех j=1,2,…,n, где  . Следовательно, выбранная строка является линейной комбинацией базисных строк. Теорема доказана. Если в системе векторов часть линейно зависима, то вся система обязательно линейно зависима. 1) Три вектора линейно зависимы тогда и только тогда, когда они компланарны.. В самом деле, пусть векторы
. Следовательно, выбранная строка является линейной комбинацией базисных строк. Теорема доказана. Если в системе векторов часть линейно зависима, то вся система обязательно линейно зависима. 1) Три вектора линейно зависимы тогда и только тогда, когда они компланарны.. В самом деле, пусть векторы  линейно зависимы. Тогда
линейно зависимы. Тогда 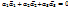 , и среди чисел
, и среди чисел  есть не равные нулю. Пусть, для определенности, не равно нулю первое число
есть не равные нулю. Пусть, для определенности, не равно нулю первое число 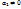 . В этом случае мы имеем право записать:
. В этом случае мы имеем право записать: 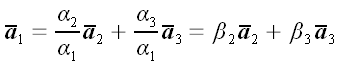 . Но это означает, что векторы
. Но это означает, что векторы  компланарны, то можно считать, что они лежат в одной плоскости. Здесь возможны варианты, которые мы рассмотрим по отдельности.
компланарны, то можно считать, что они лежат в одной плоскости. Здесь возможны варианты, которые мы рассмотрим по отдельности.  Вариант 1. Один из векторов
Вариант 1. Один из векторов 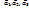 является нулевым вектором. Пусть, для определенности, это будет первый вектор. В этом случае мы можем записать:
является нулевым вектором. Пусть, для определенности, это будет первый вектор. В этом случае мы можем записать:  Вариант 2. Среди векторов
Вариант 2. Среди векторов  нет нулевых векторов, но есть коллинеарные. Пусть, для определенности, коллинеарными являются первые два вектора. Но в этом случае, первый вектор может быть выражен через второй:
нет нулевых векторов, но есть коллинеарные. Пусть, для определенности, коллинеарными являются первые два вектора. Но в этом случае, первый вектор может быть выражен через второй: 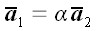 , и, следовательно,
, и, следовательно,  . Вариант 3. Среди векторов
. Вариант 3. Среди векторов  , и мы снова получаем, что:
, и мы снова получаем, что:  . 2) Любые четыре вектора в трехмерном пространстве всегда линейно зависимы. Здесь также возможны два варианта. Вариант 1. Какие либо три вектора являются компланарными. Пусть, для определенности, этими векторами будут первые три. В этом случае мы можем подобрать не все равные нулю числа
. 2) Любые четыре вектора в трехмерном пространстве всегда линейно зависимы. Здесь также возможны два варианта. Вариант 1. Какие либо три вектора являются компланарными. Пусть, для определенности, этими векторами будут первые три. В этом случае мы можем подобрать не все равные нулю числа  . Но тогда.
. Но тогда.  Вариант 2. Любые три вектора не являются компланарными. В этом случае любой из четырех векторов может быть разложен по остальным трем как по базису
Вариант 2. Любые три вектора не являются компланарными. В этом случае любой из четырех векторов может быть разложен по остальным трем как по базису  , и мы можем записать, чт
, и мы можем записать, чт  . Следовательно, в обоих возможных случаях четыре вектора являются линейно зависимыми. Мы также показали, что в плоскости любые три вектора являются линейно зависимыми, в то же время в плоскости всегда можно найти два линейно независимых вектора, так как для этого достаточно, чтобы они не были коллинеарные.
. Следовательно, в обоих возможных случаях четыре вектора являются линейно зависимыми. Мы также показали, что в плоскости любые три вектора являются линейно зависимыми, в то же время в плоскости всегда можно найти два линейно независимых вектора, так как для этого достаточно, чтобы они не были коллинеарные.


