(0,0,….,0)- для неё справедливо 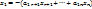
……………………………………………….. (5`)
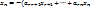
Свойства множества решений однородной системы уравнений выражены в предложениях. Предложение 1. Если столбцы 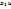
 –решения однородной системы, то их сумма
–решения однородной системы, то их сумма  удовлетворяет решение. Произведение решения на любое число тоже будет решением.
удовлетворяет решение. Произведение решения на любое число тоже будет решением.
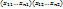 -решение.
-решение.

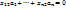

 , где
, где 
Предожение 2.
Если ранг матрицы однородной системы =r, то система имеет (n-r) –линейно-независимое решений.
Придадим параметрические неизвестные (n-r) значений, т.е.
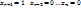
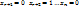
……………………………………………
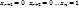
 =
= 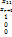
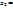
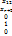
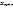 =
= 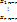 (10)
(10)
(10)-нормальная фундаментальная система решени. Любая система из (n-r) –линейно-независимых решений называется фундаментальным решением системы.Предложение 5. Пусть ( -произвольное фундаментальное решение однородной системы, тогда любое решение x представляет собой линейную комбинацию решений (
-произвольное фундаментальное решение однородной системы, тогда любое решение x представляет собой линейную комбинацию решений (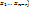 . Док-во: составим матрицу X, столбцы которой являются решением X=(
. Док-во: составим матрицу X, столбцы которой являются решением X=( , т.к. в ней есть лиейно-независимые столбцы. Rg
, т.к. в ней есть лиейно-независимые столбцы. Rg 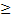 (n-r), т.к. в ней есть (n-r) линейно-независимый столбцов, или Rg
(n-r), т.к. в ней есть (n-r) линейно-независимый столбцов, или Rg  (n-r), т.к.
(n-r), т.к.  выржается через параметрические неизвестные, причем коэффициент одинаковый для каждого столбца.
выржается через параметрические неизвестные, причем коэффициент одинаковый для каждого столбца.  фундаментальая система решений однородной системы
фундаментальая система решений однородной системы
x= 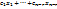 (11), т.е.
(11), т.е.
 =
=  +…+
+…+ 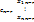 (11)
(11)
Это решение(каковыми бы не были числа 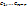 ) столбец x определяется (11) и является решением.
) столбец x определяется (11) и является решением.
47.Произведение матриц. Обратная матрица. Пусть a=(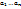 )=
)= 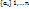 ; b=
; b= 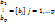 ; a*b-назвается число суммы произведений с одинаковыми номерами. Пусть матрица А (m*n) и матрица В (n*p).Матрица такова, что длина строки=высоте столбца. Умножим каждую строку a на каждый столбец b. Получим m*p произведение. Запишем мат. С (m*p), каждый столбец мат. С состоит произведений строк a на b. Любая строка С состоит из произведения строк a на имеющий один и тот же номер на любой b.
; a*b-назвается число суммы произведений с одинаковыми номерами. Пусть матрица А (m*n) и матрица В (n*p).Матрица такова, что длина строки=высоте столбца. Умножим каждую строку a на каждый столбец b. Получим m*p произведение. Запишем мат. С (m*p), каждый столбец мат. С состоит произведений строк a на b. Любая строка С состоит из произведения строк a на имеющий один и тот же номер на любой b. 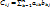 , где i=1,…m, 1,…p. (1)Определение. Матрица С, которая выражается через элементы мат. А и В по формуле(1) назовем произведением Аи В и обозначается А*В.
, где i=1,…m, 1,…p. (1)Определение. Матрица С, которая выражается через элементы мат. А и В по формуле(1) назовем произведением Аи В и обозначается А*В.
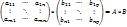
Предложение 1. j- столбец мат. А*В, есть лин. комбинация столбца мат. А с коэффициентами j-го столбца мат. В. i-строк мат. А*В, есть лин. комбинация строк мат. В с коэффициентами i-ой строки мат. А. Обозначим А(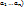 , B(
, B( и С(
и С(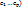 . Отметим, что столбцы мат. А и А*В имеют одинаковую высоту, поскольку для получения
. Отметим, что столбцы мат. А и А*В имеют одинаковую высоту, поскольку для получения 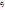 последовательно умножается строки А на
последовательно умножается строки А на 
Свойства умножения матрицы: А*В≠В*А-некоммуникативно, если же А*В=В*А- матрицы называюся перестановочными.
Свойства операций: Предложение 2.-умножение матриц ассоциативно, т.е. если определены А*В и (А*В)*С, то определены В*С и А*(В*С); (А*В)*С=А*(В*С)
Предложение 3. -умножене матриц дистрибутивно, если А*(В+С)-имеет смысл. А*(В+С)=А*В+А*С;(А+В)*С=А*С+В*С. Если произведение матриц А*В имеет смысл, то 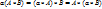 Предложение 4. Ранг произведение матриц не превосходит ранга сомножетелей. Rg(A*B) ≤RgA; Rg(A*B)≤ RgB; D=(A\A*B), очевидно, что Rg(A*B) ≤RgD. Предложение 5. Если определено произведение матриц А*В, то определено и произведение ВТ*АТ; (А*В)Т=ВТ*АТ
Предложение 4. Ранг произведение матриц не превосходит ранга сомножетелей. Rg(A*B) ≤RgA; Rg(A*B)≤ RgB; D=(A\A*B), очевидно, что Rg(A*B) ≤RgD. Предложение 5. Если определено произведение матриц А*В, то определено и произведение ВТ*АТ; (А*В)Т=ВТ*АТ
Следствие. (А*В*С)Т=АТ*ВТ*СТ; Док-во: (А*В)Т= СТ*(А*В)Т= АТ*ВТ*СТ. Доказано.
Обратная матрица. Матрица X, удовлетворяющая вместе с матрицей А условие X*A=A*X=  , где
, где  -единичная матрица некоторого порядка n. Поскольку А и А-1-перестановочные, то ои должны быть квадратными матрицами порядка n.Из предложения 2 следует, что Rg
-единичная матрица некоторого порядка n. Поскольку А и А-1-перестановочные, то ои должны быть квадратными матрицами порядка n.Из предложения 2 следует, что Rg 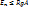 , RgA=n.Поэтому А имет обратную матрицу, тогда когда её определитель не равен 0. Это необходимое и достаточное условие существования обратной матрицы и только одну. Для каждой мат. А, где
, RgA=n.Поэтому А имет обратную матрицу, тогда когда её определитель не равен 0. Это необходимое и достаточное условие существования обратной матрицы и только одну. Для каждой мат. А, где  АX=E, при
АX=E, при 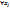 , должен удовлетворять условию,
, должен удовлетворять условию,  ;
;

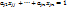 (4)
(4)
………………………………………
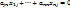
По правилу Крамера определиель этой системы отличен от нуля и система имеет одно решение. Отсюда следует, что каждый столбец системы определен единственным образом. Существует матрица Y, где X*Y=E; AX*Y=AE; EY=AE; Y=A. Этот способ позволяет найти обратную матрицу.
 , где
, где  -детерминант.
-детерминант.
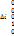
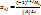 (5)-формула для вычисления обратной матрицы.;A*X=E;X=E*A-1;(A-1)-1=A (6);(AB)-1=B-1A-1(7)
(5)-формула для вычисления обратной матрицы.;A*X=E;X=E*A-1;(A-1)-1=A (6);(AB)-1=B-1A-1(7)
(AT)-1=(A-1)T(8)
48. Элементарные преобразования матриц. Каждое элементарное преобразование строк матрицы А размером (m*n)равносильно умножению матрицы А на некоторую квадратную матрицу слева размером m.Рассмотрим матрицу S1 которая получается из Еп перестановкой i-ой и j-ой строки. S2 —матрица, получаемая из единичной матрицы (единицы заменяем на α ). Из предложения 1 следует, что при умножении А на S2 слева i строка умножается на а.S2A = αА; Обозначим через S3
S
3(A)=A; Заметим, что ||S
1||=-1; ||S
2||=α;||S
3||=||A|| Для матрицы элементарных преобразований имеем det|SA| =
detS * detA
Предложение. Для любых квадратных матриц А и В одного порядка ||A*B||=||A||*||B||. Если det А=0, то из утверждения вытекает, что ||A*B|| = 0 -из оценки ранга матрицы. Если detA ≠0, то существует А-1. А-1 может быть превращена в единичную матрицу при помощи элементарных преобразований. S1 *... * SpA-1 = E; S1 *... * Sp = EA = A; ||A*B|| = ||S1*S2*...*Sp|*B|=|S1|*|S2|*...*|Sp|*|B| = ||A||*||B||
49. Элементарные преобразования как умножение матриц. Пусть даны две прямоугольные матрицы A и B размерности 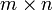 и
и 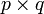 соответственно:
соответственно:
 Тогда, если число столбцов матрицы A равно числу строк матрицы B, то есть n = p, то определена матрица C размерностью
Тогда, если число столбцов матрицы A равно числу строк матрицы B, то есть n = p, то определена матрица C размерностью 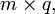 называемая их произведением:
называемая их произведением:  где:
где:  Операция умножения двух матриц выполнима только в том случае, если число столбцов в первом сомножителе равно числу строк во втором; в этом случае говорят, что форма матриц согласована. В частности, умножение всегда выполнимо, если оба сомножителя — квадратные матрицы одного и того же порядка. Следует заметить, что из существования произведения AB вовсе не следует существование произведения BA.
Операция умножения двух матриц выполнима только в том случае, если число столбцов в первом сомножителе равно числу строк во втором; в этом случае говорят, что форма матриц согласована. В частности, умножение всегда выполнимо, если оба сомножителя — квадратные матрицы одного и того же порядка. Следует заметить, что из существования произведения AB вовсе не следует существование произведения BA.
Свойства:Сочетательное свойство: 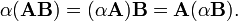 Распределительное свойство:
Распределительное свойство: 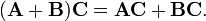 Произведение матрицы на единичную матрицу Е подходящего порядка равно самой матрице
Произведение матрицы на единичную матрицу Е подходящего порядка равно самой матрице 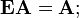 Произведение матрицы на нулевую матрицу 0 подходящей размерности равно нулевой матрице:
Произведение матрицы на нулевую матрицу 0 подходящей размерности равно нулевой матрице: 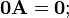
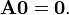 Если А и В — квадратные одного и того же порядка, то произведение матриц обладает ещё рядом свойств. Умножение матриц в целом некоммутативно:
Если А и В — квадратные одного и того же порядка, то произведение матриц обладает ещё рядом свойств. Умножение матриц в целом некоммутативно: 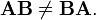 Если
Если 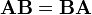 , то матрицы А и В называются перестановочными или коммутирующими между собой. Определитель и след произведения не зависят от порядка умножения матриц:
, то матрицы А и В называются перестановочными или коммутирующими между собой. Определитель и след произведения не зависят от порядка умножения матриц: 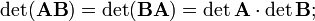
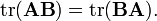
50. определитель произведения матриц. Для любых двух квадратных матриц одного порядка 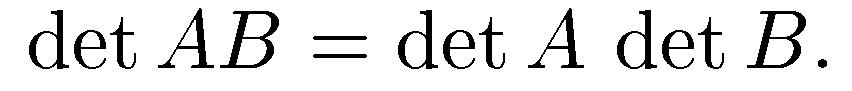 Док-во. Пусть матрица А невырождена. Разложим ее в произведение элементарных матриц. Тогда
Док-во. Пусть матрица А невырождена. Разложим ее в произведение элементарных матриц. Тогда 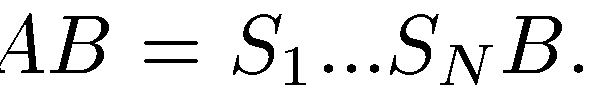 .последовательно применяя формулу
.последовательно применяя формулу 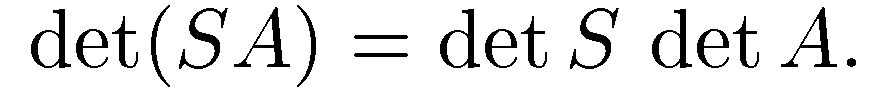 , получим
, получим 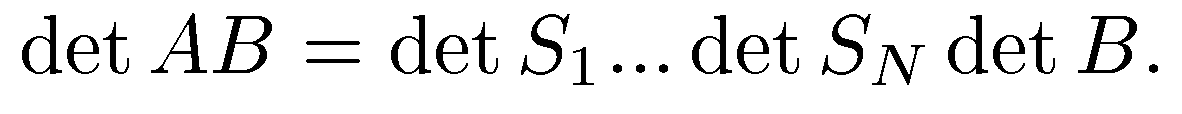 теперь из формулы
теперь из формулы  следует утверждение. Если матрица А вырождена,то по предложению(если хоть одна из матриц А и В вырождена, то произведение АВ-вырожденная матрица)произведение АВ также вырождена и detАВ равен нулю так же,как и detA detB
следует утверждение. Если матрица А вырождена,то по предложению(если хоть одна из матриц А и В вырождена, то произведение АВ-вырожденная матрица)произведение АВ также вырождена и detАВ равен нулю так же,как и detA detB

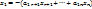
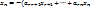
 –решения однородной системы, то их сумма
–решения однородной системы, то их сумма  удовлетворяет решение. Произведение решения на любое число тоже будет решением.
удовлетворяет решение. Произведение решения на любое число тоже будет решением.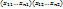 -решение.
-решение.
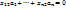

 , где
, где 
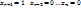
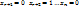
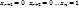
 =
= 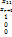
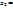
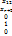
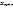 =
= 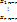 (10)
(10) -произвольное фундаментальное решение однородной системы, тогда любое решение x представляет собой линейную комбинацию решений (
-произвольное фундаментальное решение однородной системы, тогда любое решение x представляет собой линейную комбинацию решений (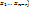 . Док-во: составим матрицу X, столбцы которой являются решением X=(
. Док-во: составим матрицу X, столбцы которой являются решением X=( , т.к. в ней есть лиейно-независимые столбцы. Rg
, т.к. в ней есть лиейно-независимые столбцы. Rg 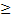 (n-r), т.к. в ней есть (n-r) линейно-независимый столбцов, или Rg
(n-r), т.к. в ней есть (n-r) линейно-независимый столбцов, или Rg  (n-r), т.к.
(n-r), т.к.  выржается через параметрические неизвестные, причем коэффициент одинаковый для каждого столбца.
выржается через параметрические неизвестные, причем коэффициент одинаковый для каждого столбца.  фундаментальая система решений однородной системы
фундаментальая система решений однородной системы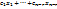 (11), т.е.
(11), т.е. =
=  +…+
+…+ 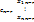 (11)
(11)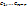 ) столбец x определяется (11) и является решением.
) столбец x определяется (11) и является решением.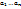 )=
)= 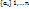 ; b=
; b= 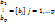 ; a*b-назвается число суммы произведений с одинаковыми номерами. Пусть матрица А (m*n) и матрица В (n*p).Матрица такова, что длина строки=высоте столбца. Умножим каждую строку a на каждый столбец b. Получим m*p произведение. Запишем мат. С (m*p), каждый столбец мат. С состоит произведений строк a на b. Любая строка С состоит из произведения строк a на имеющий один и тот же номер на любой b.
; a*b-назвается число суммы произведений с одинаковыми номерами. Пусть матрица А (m*n) и матрица В (n*p).Матрица такова, что длина строки=высоте столбца. Умножим каждую строку a на каждый столбец b. Получим m*p произведение. Запишем мат. С (m*p), каждый столбец мат. С состоит произведений строк a на b. Любая строка С состоит из произведения строк a на имеющий один и тот же номер на любой b. 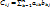 , где i=1,…m, 1,…p. (1)Определение. Матрица С, которая выражается через элементы мат. А и В по формуле(1) назовем произведением Аи В и обозначается А*В.
, где i=1,…m, 1,…p. (1)Определение. Матрица С, которая выражается через элементы мат. А и В по формуле(1) назовем произведением Аи В и обозначается А*В.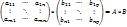
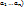 , B(
, B( и С(
и С(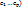 . Отметим, что столбцы мат. А и А*В имеют одинаковую высоту, поскольку для получения
. Отметим, что столбцы мат. А и А*В имеют одинаковую высоту, поскольку для получения 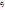 последовательно умножается строки А на
последовательно умножается строки А на 
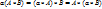 Предложение 4. Ранг произведение матриц не превосходит ранга сомножетелей. Rg(A*B) ≤RgA; Rg(A*B)≤ RgB; D=(A\A*B), очевидно, что Rg(A*B) ≤RgD. Предложение 5. Если определено произведение матриц А*В, то определено и произведение ВТ*АТ; (А*В)Т=ВТ*АТ
Предложение 4. Ранг произведение матриц не превосходит ранга сомножетелей. Rg(A*B) ≤RgA; Rg(A*B)≤ RgB; D=(A\A*B), очевидно, что Rg(A*B) ≤RgD. Предложение 5. Если определено произведение матриц А*В, то определено и произведение ВТ*АТ; (А*В)Т=ВТ*АТ , где
, где  -единичная матрица некоторого порядка n. Поскольку А и А-1-перестановочные, то ои должны быть квадратными матрицами порядка n.Из предложения 2 следует, что Rg
-единичная матрица некоторого порядка n. Поскольку А и А-1-перестановочные, то ои должны быть квадратными матрицами порядка n.Из предложения 2 следует, что Rg 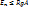 , RgA=n.Поэтому А имет обратную матрицу, тогда когда её определитель не равен 0. Это необходимое и достаточное условие существования обратной матрицы и только одну. Для каждой мат. А, где
, RgA=n.Поэтому А имет обратную матрицу, тогда когда её определитель не равен 0. Это необходимое и достаточное условие существования обратной матрицы и только одну. Для каждой мат. А, где  АX=E, при
АX=E, при 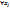 , должен удовлетворять условию,
, должен удовлетворять условию,  ;
;
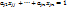 (4)
(4)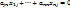
 , где
, где  -детерминант.
-детерминант.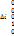
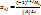 (5)-формула для вычисления обратной матрицы.;A*X=E;X=E*A-1;(A-1)-1=A (6);(AB)-1=B-1A-1(7)
(5)-формула для вычисления обратной матрицы.;A*X=E;X=E*A-1;(A-1)-1=A (6);(AB)-1=B-1A-1(7)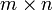 и
и 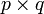 соответственно:
соответственно: Тогда, если число столбцов матрицы A равно числу строк матрицы B, то есть n = p, то определена матрица C размерностью
Тогда, если число столбцов матрицы A равно числу строк матрицы B, то есть n = p, то определена матрица C размерностью 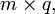 называемая их произведением:
называемая их произведением:  где:
где:  Операция умножения двух матриц выполнима только в том случае, если число столбцов в первом сомножителе равно числу строк во втором; в этом случае говорят, что форма матриц согласована. В частности, умножение всегда выполнимо, если оба сомножителя — квадратные матрицы одного и того же порядка. Следует заметить, что из существования произведения AB вовсе не следует существование произведения BA.
Операция умножения двух матриц выполнима только в том случае, если число столбцов в первом сомножителе равно числу строк во втором; в этом случае говорят, что форма матриц согласована. В частности, умножение всегда выполнимо, если оба сомножителя — квадратные матрицы одного и того же порядка. Следует заметить, что из существования произведения AB вовсе не следует существование произведения BA.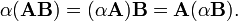 Распределительное свойство:
Распределительное свойство: 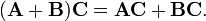 Произведение матрицы на единичную матрицу Е подходящего порядка равно самой матрице
Произведение матрицы на единичную матрицу Е подходящего порядка равно самой матрице 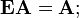 Произведение матрицы на нулевую матрицу 0 подходящей размерности равно нулевой матрице:
Произведение матрицы на нулевую матрицу 0 подходящей размерности равно нулевой матрице: 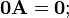
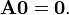 Если А и В — квадратные одного и того же порядка, то произведение матриц обладает ещё рядом свойств. Умножение матриц в целом некоммутативно:
Если А и В — квадратные одного и того же порядка, то произведение матриц обладает ещё рядом свойств. Умножение матриц в целом некоммутативно: 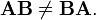 Если
Если 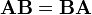 , то матрицы А и В называются перестановочными или коммутирующими между собой. Определитель и след произведения не зависят от порядка умножения матриц:
, то матрицы А и В называются перестановочными или коммутирующими между собой. Определитель и след произведения не зависят от порядка умножения матриц: 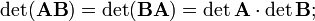
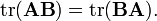
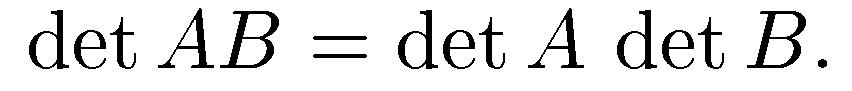 Док-во. Пусть матрица А невырождена. Разложим ее в произведение элементарных матриц. Тогда
Док-во. Пусть матрица А невырождена. Разложим ее в произведение элементарных матриц. Тогда 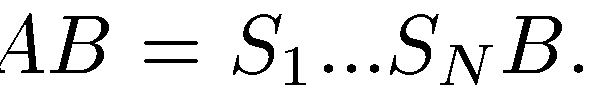 .последовательно применяя формулу
.последовательно применяя формулу 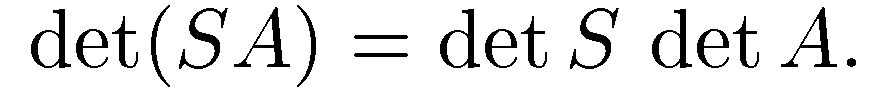 , получим
, получим 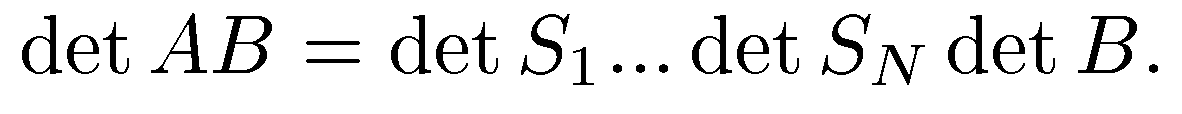 теперь из формулы
теперь из формулы  следует утверждение. Если матрица А вырождена,то по предложению(если хоть одна из матриц А и В вырождена, то произведение АВ-вырожденная матрица)произведение АВ также вырождена и detАВ равен нулю так же,как и detA detB
следует утверждение. Если матрица А вырождена,то по предложению(если хоть одна из матриц А и В вырождена, то произведение АВ-вырожденная матрица)произведение АВ также вырождена и detАВ равен нулю так же,как и detA detB


