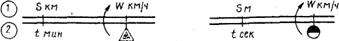Глава 4 НАВИГАЦИОННАЯ ЛИНЕЙКА
1. Назначение и принцип устройства навигационной линейки НЛ-10М
Навигационная линейка НЛ-10М является счетным инструментом пилота и штурмана и предназначена для выполнения необходимых расчетов при подготовке к полету и в полете. Она устроена по принципу обычной счетной логарифмической линейки и позволяет заменить сложные математические действия над числами (умножение и деление) более простыми действиями — сложением и вычитанием отрезков шкал, выражающих в определенном масштабе логарифмы этих чисел. Навигационная линейка состоит из корпуса, движка и визирки. На корпусе и движке нанесены шкалы, индексы, формулы и надписи. НЛ-10М позволяет решать следующие основные задачи: 1. Расчет элементов (УС, W, МК и t) по известному ветру. 2. Определение скорости и направления ветра. 3. Определение пройденного расстояния, скорости и времени полета. 4. Учет методических ошибок барометрических высотомеров и указателей воздушной скорости. 5. Определение радиуса виража и времени разворота на 360° и на заданный угол. 6. Определение значений тригонометрических функций, умножение и деление чисел на тригонометрические функции углов. Кроме того, НЛ-10М позволяет решать многие специальные и математические задачи. 2. Шкалы навигационной линейки и их назначение
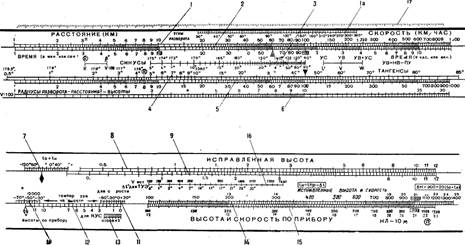
Навигационная линейка имеет не равномерные шкалы, а логарифмические. При решении задач с помощью НЛ-10М используется одновременно две, а иногда и больше шкал, которые называются смежными. На навигационной линейке нанесены следующие шкалы (рис. 4.1). Шкала 1 — расстояний и скоростей. Шкала 2 — времени. На шкале 2 нанесено четыре индекса: круглый, треугольный и два прямоугольных. Шкалы 1 и 2 служат для определения пройденного расстояния, скорости, времени полета и для решения задач на умножение и деление чисел. Шкала 1 а — углов разворота; она используется совместно со шкалами 1 и 2 для определения времени разворота самолета на заданный угол. Шкала 3 — синусов, шкала 4 — тангенсов и шкала 5 — радиусов разворота, расстояний и высот. На шкале 4 нанесены треугольный и круглый индексы с буквой R. Эти шкалы предназначены для определения тригонометрических функций углов и для выполнения действий с тригонометрическими функциями (решаются прямоугольные и косоугольные треугольники). Шкала 6 является дополнительной и используется совместно со шкалами 4 и 5 для определения радиуса разворота, извлечения квадратных корней из чисел и возведения чисел в квадрат. Шкала 7 —суммы температур у земли и на высоте полета, шкала 8 — исправленных высот и шкала 9 — высот по прибору
Эти шкалы предназначены для учета методических температурных поправок в показания барометрических высотомеров. Шкала 10 — температуры воздуха для высот более 12000 м, шкала 11 — температуры воздуха на высоте для определения скорости, шкала 12 — высот по прибору, шкала 13 — высот по прибору для КУС, шкала 14 — исправленных -высот и скоростей и шкала 15 — высот и скоростей по прибору. На шкале 14 нанесено три индекса: AM, MM и ФУТЫ. Шкалы 10, 11, 12, 13, 14 и 15 предназначены для пересчета высот и скоростей полета, а шкалы 14 и 15, кроме того, для перевода морских и английских миль в километры и футов в метры и обратно. Шкала 16 — поправок к показанию термометра наружного воздуха типа ТУЭ и шкала 17 — масштабная миллиметровая шкала, предназначенная для измерения расстояний на карте.
3. Умножение и деление чисел при помощи НЛ-10М
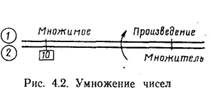
Умножение и деление чисел на НЛ-10М выполняется по шкалам 1 и 2 или 14 и 15. При пользовании этими шкалами значения чисел, нанесенных на них, можно увеличивать или уменьшать в любое число раз, кратное десяти. Для умножения чисел по шкалам 1 и 2 необходимо прямоугольный индекс с цифрой.10 или 100 шкалы 2 установить на множимое, а пробив множителя отсчитать по шкале 1 искомое произведение. Положение шкал линейки при решении различных задач принято изображать в виде ключей. Ключ для умножения чисел показан на рис. 4.2.
Определение количества знаков произведений осуществляется путем определения приближенного ответа в уме или по правилам умножения чисел на логарифмической линейке. Для деления чисел необходимо делитель, взятый по шкале 2, установить на делимое по шкале 1 и против прямоугольного индекса с цифрой 10 или 100 отсчитать по шкале 1 искомое частное.
4. Определение значений тригонометрических функций углов
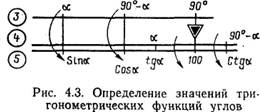
Значения синуса и косинуса данного угла α на НЛ-10М определяются по шкалам 3 и 5, значения тангенса и котангенса — по шкалам 4 и 5. Чтобы определить синус и косинус данного угла, необходимо 90° шкалы 3 или треугольный индекс шкалы 4 установить на деление 100 шкалы 5 и с помощью риски визирки отсчитать против значения данного угла α шкалы 3 по шкале 5 искомое значение синуса (в долях единицы). Значение косинуса угла α отсчитывается против угла 90° — α (рис. 4.3).
Для определения тангенса и котангенса угла треугольный индекс шкалы 4 необходимо установить на деление 100 шкалы 5 и против значения заданного угла α шкалы 4 отсчитать на шкале 5 искомое значение тангенса, а против значений 90°—αотсчитать искомое значение котангенса (см. рис. 4.3).
Пример. Дан угол α=40°. Определить синус, косинус, тангенс и котангенс этого угла. Решение, sin 40°=0,64; cos 40°=0,77; tg 40°=0,84; ctg 40°= 1,19. 5. Умножение данного числа на тригонометрические функции углов
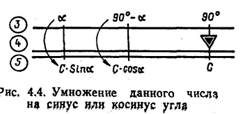
Умножение данного числа на синус и косинус угла на НЛ-10М производится по шкалам 3 и 5, а умножение на тангенс и котангенс угла — по шкалам 4 и 5. Для умножения числа на синус и косинус угла а необходимо 90° шкалы 3 или треугольный индекс шкалы 4 установить на заданное число и против угла αшкалы 3 отсчитать на шкале 5 искомое произведение числа на синус угла α, a против угла 90° — α — искомое произведение числа на косинус угла α (рис. 4.4).
Пример. Дан угол α = 42°; число С=250. Определить произведение числа 250 на синус и косинус 42°. Решение. 250. sin 42°= 167; 260. cos 42° =186.
Для умножения числа на тангенс и котангенс угла α необходимо треугольный индекс шкалы 4 установить на заданное число и против угла а шкалы 4 отсчитать на шкале 5 искомое произведение числа на тангенс угла, α против угла 90°—α—искомое произведение числа на котангенс угла а. Пример. Дан угол α=42°; число С=250. Определить произведение числа 260 на тангенс и котангенс 42°. Решение: 250-tg 42°=225; 250-ctg 42°=277.
6. Деление данного числа на тригонометрические функции углов
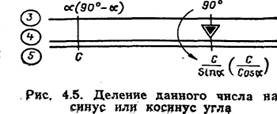
Деление данного числа на тригонометрические функции углов выполняется с помощью тех же шкал, что и умножение числа на тригонометрические функции углов. Для деления заданного числа на синус или косинус угла на НЛ-10М необходимо установить риску визирки на заданное число по шкале 5, затем подвести против риски визирки значение заданного угла α шкалы 3 (при делении числа на синус угла) или угла 90° — α(при делении числа на косинус α)и против треугольного индекса шкалы 4 отсчитать на шкале 5 искомое частное (рис. 4.5).
Пример. Дан угол α=50°; число равно 250. Определить частное от деления 250 на синус и косинус угла 50°. Решение. 250: sin 50°=326; 250: cos 50° = 389. Чтобы разделить число на тангенс угла α, на НЛ-10М необходимо деление угла αшкалы 4 совместить с делением заданного числа шкалы 5 и против треугольного индекса шкалы 4 отсчитать на шкале 5 искомое частное. При делении числа на котангенс угла α против заданного числа подводят деление 90°—α. Пример. Дан угол α=40°; число С=160. Определить частное от деления 160 на тангенс и котангенс 40°. Решение. 160:tg40°=191; 160:ctg40°= 134. 7. Расчет пройденного расстояния, времени полета и путевой скорости
Пройденное расстояние определяется по формуле S = Wt, где S—пройденное расстояние, км (м); W — путевая скорость, км/ч; t — время полета, ч и мин (мин и сек). Для определения пройденного расстояния на НЛ-10М необходимо установить треугольный индекс шкалы 2 на значение путевой скорости по шкале 1 и против деления шкалы 2, соответствующего времени полета, отсчитать на шкале 1 искомое расстояние в километрах (рис. 4.6).
Рис. 4.6. Определение пройденного расстояния
Пример. W=420 км/ч; t= 9 мин. Определить пройденное расстояние S. Решение. S=63 км. Если время полета выражено в секундах, то пройденное расстояние определяется в таком порядке: установить круглый индекс шкалы 2 на значение путевой скорости по шкале 1 и против деления шкалы 2, соответствующего времени полета, отсчитать на шкале 1 искомое расстояние в метрах или километрах (см. рис. 4.6). Пример. W=300 км/ч; t=45 сек. Определить пройденное расстояние S. Решение. S=3750 м. Время полета определяется по формуле t= Чтобы определить время полета на НЛ-10М, необходимо треугольный индекс шкалы 2 установить на значение путевой скорости по шкале 1 и против деления шкалы 1, соответствующего данному расстоянию, отсчитать по шкале 2 искомое время полета. Пример. W =510 км/ч; S = 187 км. Определить время полета t. Решение. t=22 мин. Если данное расстояние выражено в метрах, то время полета определяется в таком порядке: установить круглый индекс шкалы 2 на значение путевой скорости по шкале и против деления шкалы 1, соответствующего данному расстоянию, отсчитать искомое время полета. Пример. W =270 км/ч; S = 4900 м. Определить время полета. Решение. t= 65 сек.
Путевая скорость определяется по формуле W = Для определения путевой скорости на НЛ-10М необходимо установить риску визирки против деления шкалы 1, соответствующего пройденному расстоянию, и подвести под риску деление шкалы 2, соответствующее времени полета, затем против треугольного индекса шкалы 2 отсчитать на шкале 1 искомое значение путевой скорости в километрах в час (рис. 4.7). Пример. S = 72 км; t= 10 мин. Определить путевую скорость. Решение. W=432 км/ч. Если пройденное расстояние небольшое и время полета выражено в секундах, то путевая скорость отсчитывается против круглого индекса. Для этого необходимо установить риску визирки на деление шкалы 1, соответствующее пройденному расстоянию, и подвести под риску деление шкалы 2, соответствующее времени полета в секундах, затем против круглого индекса шкалы 2 отсчитать
Рис. 4.7. Определение путевой скорости
на шкале 1 искомую путевую скорость в километрах в час (см. рис. 4.7). Пример. S = 3000 м; t = 20 сек. Определить путевую скорость. Решение. W =540 км/ч.
8. Перевод скорости, выраженной в метрах в секунду, в скорость, выраженную в километрах в час, и обратно
Такая операция осуществляется по формулам: V км/ч = V м/сек ·3,6; V м/сек = V км/ч:3,6. Для вычислений по этим формулам на НЛ-10М используются шкалы 1 и 2. Чтобы перевести скорость, выраженную в метрах в секунду, в скорость, выраженную в километрах в час, необходимо прямоугольный индекс 10 шкалы 2 установить на деление шкалы 1, соответствующее скорости в метрах в секунду, и против круглого индекса шкалы 2 отсчитать на шкале 1 искомое значение скорости в километрах в час (рис. 4.8).
Пример. V =12 м/сек. Перевести в километры в час. Решение. V =43 км/ч. Для перевода скорости, выраженной в километрах в час, в скорость, выраженную в метрах в секунду, необходимо круглый индекс шкалы 2 установить на деление шкалы 1, соответствующее заданной скорости в километрах в час, и против прямоугольного индекса 10 отсчитать по шкале 1 искомое значение скорости в метрах в секунду. Пример. V =480 км/ч. Перевести в метры в секунду Решение. V = 133 м/сек. 9. Перевод морских и английских миль в километры и обратно
Перевод морских (ММ) и английских (AM) миль в километры и обратно производится по формулам: Sкм= S (ММ)·1,852; Sкм = S (AM)·1,6; S (ММ) = Sкм:1,852; S (AM) = Sкм:1,6.
Чтобы перевести морские или английские мили в километры, на НЛ-10М необходимо деление 100 или 1000 шкалы 14 установить на число морских или английских миль по шкале 15 и соответственно против индекса ММ или AM.отсчитать по шкале 15 километры (рис. 4.9). Пример. 1. S = 200 морских миль. Перевести в километры. Решение: S = 370 км. Пример 2. S = 210 английских миль. Перевести в километры. Решение. S = 336 км. Для перевода километров в морские или английские мили необходимо индекс MM (AM) шкалы 14 установить по шкале 15 на данное число километров, а против деления 100 или 1000 шкалы 14 отсчитать по шкале 15 число морских или английских миль. Пример 1. S= 245 км. Перевести в морские мили. Решение. S== 132 морских мили. Пример 2. 5 = 300 км. Перевести в английские мили. Решение. 5 = 187 английских миль. 10. Перевод футов в метры и обратно
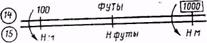
Футы переводятся в метры, а метры в футы по формулам: Hм = H футы:3,28; H футы = Н м·3,28. Чтобы перевести футы в метры, на НЛ-10М необходимо индекс ФУТЫ шкалы 14 установить по шкале 15 на данное число футов, а против деления 100 или 1000 шкалы 14 отсчитать по шкале 15 число метров рис. (4.10).
Рис. 4.10. Перевод футов в метры Пример. Н=4000 футов. Перевести в метры. Решение. Н=1220 м. При переводе метров в футы необходимо деление 100 или 1000 шкалы 14 установить на данное число метров шкалы 15 и против индекса ФУТЫ отсчитать по шкале 15 число футов. Пример. Н=3000 м. Перевести в футы. Решение. Н=9840 футов. Использование навигационной линейки при решении специальных задач самолетовождения дано в соответствующих главах настоящего учебника.
|



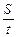 .
.