Степень неравномерности подачи
Рассматривая представленные графики подачи видно, что значения подачи меняются от некоторой минимальной величины до максимальной. Колебания подачи насоса принято оценивать отношением максимальной мгновенной подачи dΩ;макс. к средней мгновенной подаче dΩ;ср. Это отношение называют степенью неравномерности подачи ψ;: Ψ;= В случае одноцилиндрового насоса одинарного действия максимальная величина мгновенной подачи dΩ;макс. будет равна dΩ;макс.= Тогда степень неравномерности подачи в соответствии с уравнением (17) будет равна: Ψ;= где y макс. и y ср. – максимальное и среднее значение ординаты на графике подачи. Среднее значение ординаты y ср. на графике подачи может быть найдено из условия равенства площадей фигур, заключенных под кривой подачи реального насоса и под линией подачи идеального насоса. Применительно к одноцилиндровому насосу одинарного действия, график подачи которого приведен на рис. 8, площадь Ω;1, заключенная под синусоидой согласно уравнению (12), равна Ω;1= F·2r, а равновеликая ей площадь Ω;1и, заключенная под линией подачи идеального насоса, равна Ω;1и= y ср.·2 π·r. Приравнивая эти площади, получим: F·2r = y ср.2 π·r, откуда y ср= F/π;. Подставив значение y ср в уравнение (17а), получим: Ψ;= Приведенный метод вычисления степени неравномерности подачи универсален и может быть применен к поршневому или плунжерному насосу с любым числом цилиндров и различной кратностью действия. Вначале необходимо найти максимальное значение амплитуды на результирующей кривой графика подачи насоса и объем жидкости, подаваемой всеми цилиндрами насоса за один оборот кривошипного вала. Максимальная амплитуда на графике подачи может быть определена графическим или аналитическим методом. Затем, по известной подаче рассматриваемого насоса, вычисляют среднее значение ординаты графика подачи идеального насоса путём деления объёма жидкости, подаваемой всеми цилиндрами насоса за один оборот кривошипного вала на 2 πr. Завершают расчет степени неравномерности подачи по формуле (17а). Используя приведенную методику легко показать, что для одноцилиндрового насоса двойного действия этот коэффициент, при значениях диаметра штока и поршня, указанных на рис. 9, будет равен ψ;=1,71. Если же пренебречь диаметром штока, то ψ;=1,57. У трехцилиндрового насоса одинарного действия ψ;=1,047; у пятицилиндрового насоса одинарного действия этот коэффициент равен 1,016. Таким образом, степень неравномерности подачи зависит от числа цилиндров насоса, кратности их действия и от отношения диаметра штока к диаметру поршня.
|

 . (17)
. (17) , а мгновенная средняя подача – dΩ;ср.=
, а мгновенная средняя подача – dΩ;ср.=  .
. , (17а)
, (17а) =
= 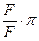 =3,14.
=3,14.


