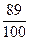Задачи на процентные отношения.
Рассмотрим более сложные задачи В13 из открытого банка заданий ЕГЭ 2012 года. В13 (99567) Четыре рубашки дешевле куртки на 8%. На сколько процентов пять рубашек дороже куртки? Решение: I способ. Пусть цена куртки - К и это 100%. Если 4 рубашки дешевле куртки на 8%, то их стоимость 100% - 8% = 92% стоимости куртки, т.е. 0,92К – стоимость четырех рубашек, тогда 0,23К ∙ 5 = 1,15К – стоимость пяти рубашек. Сравним стоимость пяти рубашек и куртки.
Ответ: 15%. II способ. Для упрощения рассуждений введем условную стоимость куртки -100 рублей. Тогда 92 рубля – стоимость 4 рубашек, 92: 4 = 23 (р) стоимость одной рубашки, 5 ∙ 23 = 115 (р) стоимость 5 рубашек.
Ответ: 15%.
В13 Брюки дороже рубашки на 30%и дешевле пиджака на 22%. На сколько процентов рубашка дешевле пиджака? I способ. Введем условную стоимость 100 рублей – стоит рубашка. Тогда 130 рублей стоят брюки. Пусть х рублей стоит пиджак. По условию задачи брюки дешевле пиджака на 22%. Зная это, составим уравнение
х – 130 = 0,22х 0,78х = 130 х = х =
Узнаем на сколько процентов рубашка дешевле пиджака.
Ответ: 40%. II способ. Пусть стоимость рубашки Р Стоимость пиджака П Стоимость брюк Б По условию задачи стоимость брюк сравнивается со стоимостью рубашки и пиджака, поэтому 0,78 П = В = 1,3 Р 0,78 П = 1.3 Р Р = Значит рубашка дешевле пиджака на 40%. Ответ: 40%.
В13 (99568) Семья состоит из мужа, жены и их дочери студентки. Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на 67%. Если бы стипендия дочери уменьшилась втрое, общий доход семьи сократился бы на 4%. Сколько процентов от общего дохода семьи составляет зарплата жены? Решение: Введем обозначения и смоделируем задачу. М – зарплата мужа Ж - зарплата жены С - зарплата дочери – студентки Д – их доход Надо ответить на вопрос Исходя из условия М + Ж + С = Д (1) 2М + Ж + С = 1,67 Д (2) М + Ж + (2) – (1): М = 0,67 Д (1) – (3): С = 0,06 Д Вернемся к равенству (1) 0,67 Д + Ж + 0,06 Д = Д 0,73 Д + Ж = Д Ж = 0,27 Д
Ответ: 27%
В13 (99569) Цена холодильника в магазине ежегодно уменьшается на одно и тоже число процентов от предыдущей цены. Определите, на сколько процентов каждый год уменьшалась цена холодильника, если выставленный на продажу за 20000 рублей, через два года был продан за 15842 рубля. Решение: I способ Пусть каждый год цена уменьшалась на х %, где 0 < х <100. (*) Через год цена станет 20000 (1 - Зная, что через два года цена станет равной 15842, составим уравнение 20000 (1 - 2 (100 – х) (100 – х) х
х = 100 х = 189, что не удовлетворяет условию (*) х = 11 Ответ: на 11%. II способ. Заметим, что цена следующего года отличается от цены предыдущего года в К раз. 20000 ∙ К К К = К = 0,89 Цена снижалась каждый год на 11%. Ответ: на 11%.
|

 - цена одной рубашки
- цена одной рубашки
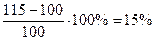
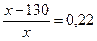
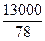
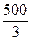

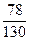 П = 0,6 П, т.е. стоимость рубашки составляет 60% от стоимости пиджака,
П = 0,6 П, т.е. стоимость рубашки составляет 60% от стоимости пиджака, -?
-?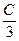 = 0,96 Д (3)
= 0,96 Д (3)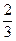 ∙ С = 0,04 Д
∙ С = 0,04 Д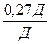 ∙ 100% = 27%
∙ 100% = 27%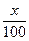 ), через два года 20000 (1 -
), через два года 20000 (1 -  .
.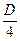 = 7921 = 89
= 7921 = 89  89
89