Основные теоретические понятия
Процент от некоторой величины – это одна сотая ее часть. Для обозначения слова «процент» применяется знак %. 1% - это Найдем 1% от 200 р., т. е. Найдем 22% от 6 кг: сначала найдем 1% от 6 кг, получим теперь найдем 22%:
Итак, чтобы найти 1% от величины, надо эту величину разделить на 100 или умножить на 0,01. Чтобы найти р% от величины, надо 1% от величины умножить на число р. Примеры Найдите 8% от 100 17% от 2000 120 % от 20 Задача За год банк начисляет на вклад «Срочный» 12 % от вложенной суммы. Сколько рублей будет начислено на вклад в 5000 рублей? Решение: 5000 р. – 100%, через год число процентов будет 100% + 12% = 112%, найдем 112% от 5000 р. известным нам способом.
Решить эту задачу можно проще. 112 % =1,12. 5000∙1,12 =5600 (р) Итак, если число а увеличивается на р %, то надо а ∙ (1+ Примеры Начертите в тетради отрезок длиной 20 клеток. а) Увеличьте его на 10 %. б) Уменьшите его на 20 %. Как найти процентное отношение двух чисел? Сколько процентов составляет число 18 от 72? Сначала найдем какую часть составляет 18 от 72. Для этого
Итак, чтобы найти сколько процентов составляет одно число от другого, надо их отношение заменить процентом, т. е. умножить полученную дробь на 100 %.
Примеры Сколько процентов от числа 80 составляет число 160? Решение: Вычислите 10 % от числа (8,7 – 4,9 – 3.2) Наряду с задачами на нахождение процента от числа, часто надо найти число по его проценту. Рассмотрим пример. Найдите число 36 % которого равны 216. Пусть это число х, тогда 36 % от х равны 0,36 х. По условию задачи, составим уравнение 0,36х = 216 х = 216: 0,36 х =21600: 36 х = 600
|

 = 0,01 величины.
= 0,01 величины.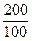 = 2, значит 1% от 200 рублей равен 2 рублям.
= 2, значит 1% от 200 рублей равен 2 рублям. =
=  (кг);
(кг);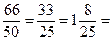 1,32 (кг)
1,32 (кг) 50∙112 = 5600 (р)
50∙112 = 5600 (р) р), аналогично, если число а уменьшается на р%, то надо а ∙(1 -
р), аналогично, если число а уменьшается на р%, то надо а ∙(1 - 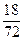 =
= 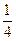 и выражаем в процентах.
и выражаем в процентах. ∙; 100 % = 200 %
∙; 100 % = 200 %


