Ввод уравнений. Дополнительная информация.

Рассмотрим несложную дополнительную модель: одномерное движение материальной точки с массой m под действием вынуждающей силы F и вязкого трения с коэффициентом mu Путь к готовому примеру «Модели\Движение\Движение.mvb»).

Уравнение движения может быть записано в естественной «физической» форме

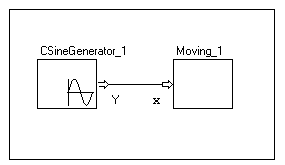
Рис 4.95

Вынуждающая сила подается на вход с генератора синусоидального сигнала (Рис 4.10Рис 4.6), поэтому искомой переменной однозначно является переменная x.

Рис 4.106

Транслятор сам преобразует это уравнение к «канонической» форме, необходимой для численного решения. Вы можете посмотреть на это представление с помощью команды «Показать уравнения в канонической форме» всплывающего меню. Для данного уравнения это будет

x: d(x)/dt = x';

x': d(x')/dt = x'';

x'': m*x'' = F-mu*x';

(перед двоеточием показана переменная, которая определяется из этого уравнения).

В данной версии пакета производные видимы только в пределах данной системы уравнений (это означает, что нельзя, например, использовать скорость в действиях перехода или в теле функции).

Теперь, не меняя уравнения движения, сделаем входной переменной x, а не F (Рис 4.12Рис 4.7).

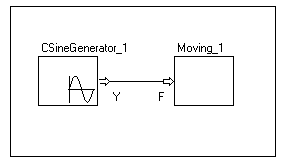
Рис 4.127

Теперь искомой переменной является сила F (то есть, мы решаем обратную задачу: какую силу нужно прикладывать, чтобы тело двигалось по синусоиде). Однако, для этой задачи мы будем иметь совсем иную «каноническую» систему уравнений:

x': x' = d(x)/dt;

x'': x'' = d(x')/dt;

F: m*x'' = F-mu*x';

Для определения силы необходимо двойное дифференцирование переменной x. Поскольку в данной версии пакета аналитические преобразования не поддерживаются, сделать это можно только с помощью численного дифференцирования. Это очень плохо для большинства численных методов и поэтому транслятор предупреждает пользователя.