Создаем гибридную модель.

 

В качетсве типовой гибридной рассмотрим модель отрывающегося маятника. Новый проект мы будем создавать на основе рассмотренного выше проекта «Маятник.mvb». Для этого с помощью команды «Проект/Сохранить как» сохраним этот проект как «ОтрывающийсяМаятник.mvb» и далее будем редактировать уже существующий класс «Маятник». Несколько позже будет рассмотрено как создать для отрывающегося маятника новый класс в том же проекте, унаследовав нужные свойства от простого маятника.

Путь к готовому примеру «Модели\Маятник\ОтрывающийсяМаятник.mvb».

 

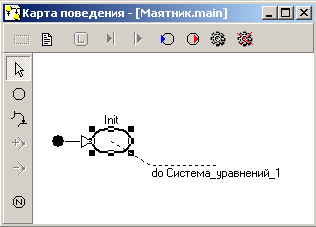
Это модель изолированной системы с несколькими качественными состояниями. Поэтому класс, создаваемый по умолчанию при открытии нового проекта, для нее подходит не вполне. Напомним, что при открытии нового проекта в создаваемом по умолчанию классе автоматически создается «Система_уравнений_1», которая приписывается начальному состоянию Init в главной карте поведения. «Система_уравнений_1» нам еще пригодится, а вот приписывание ее даму состоянию в данном случае не нужно. Выделим узел Init в главной карте поведения (Рис 6.1Рис 6.1) и с помощью кнопки или команды «Установить пустое локальное поведение» всплывающего меню сделаем узел Init пустым.

 

Рис 6.1

Учитывая, что узел Init унаследован от родительского класса CDevice и ни удалить, ни переименовать в данной версии пакета его нельзя, можно рекомендовать две «стратегии» построения главной карты поведения гибридной модели:

Рис 6.32

 

Рис 6.43

 

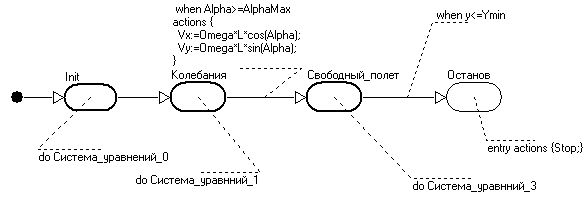
1) Стоится новая «Карта_поведения_1» (Рис 6.4Рис 6.3), которая приписывается узлу Init (Рис 6.3Рис 6.2).

2) Узел Init по-прежнему используется как начальный с безусловным переходом в узел, соответствующий первому содержательному состоянию модели - в данном случае это состояние «Колебания» (Рис 6.5Рис 6.4). Этот подход удобен в том случае, когда вычисление согласованных начальных значений переменных является нетривиальной процедурой, связанной, например, с однократным решением системы алгебраических уравнений. В этом случае начальную последовательность формул удобно помещать во входных действиях начального узла, а начальную систему алгебраических уравнений приписывать начальному узлу как непрерывное поведение. Важно уяснить, что даже если длительность пребывания в каком-либо состоянии равна нулю в непрерывном времени)вход в состояние и выход из состояния происходят в одной «временной щели»), то алгебраическая составляющая системы уравнений, приписанной этому состоянию, все равно будет решена! На Рис 6.5Рис 6.4 показано вычисление начальных значений в начальном узле Init.

 

Рис 6.54

 

В любом случае для описания гибридного поведения вам придется создавать новую карту поведения или модифицировать главную.

Далее в этом примере мы будем использовать подход, показанный на Рис 6.3Рис 6.2, Рис 6.4Рис 6.3.