Кручение с изгибом
Вид нагружения, при котором брус подвергается одновременно действию скручивающих и изгибающих моментов, называется изгибом с кручением. При расчете воспользуемся принципом независимости действия сил. Определим напряжения по отдельности при изгибе и кручении. При изгибе в поперечном сечении возникают нормальные напряжения, достигающие максимального значения в крайних волокнах
Нормальные и касательные напряжения одновременно достигают наибольшего значения в точках А и В сечения вала (рис.7.6).
Условие прочности по третьей гипотезе прочности (гипотезе наибольших касательных напряжений) Учитывая, что
Если изгиб вала происходит в двух плоскостях, то условие прочности будет Используя четвертую (энергетическую) гипотезу прочности после подстановки s и t получим Кручение и растяжение или сжатие. Сочетание деформаций кручения и растяжения испытывают, например, болты и крепёжные винты, а сочетание кручения и сжатия – винты домкратов и т.д. Нормальные и максимальные касательные напряжения в этих случаях вычисляют по формулам
Применив третью теорию прочности, получим расчётную формулу:
Применив пятую теорию прочности, получим:
|

 .
.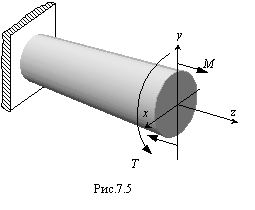 При кручении в поперечном сечении возникают касательные напряжения, достигающие наибольшего значения в точках сечения у поверхности вала
При кручении в поперечном сечении возникают касательные напряжения, достигающие наибольшего значения в точках сечения у поверхности вала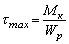 .
.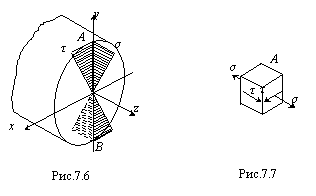 Рассмотрим напряженное состояние в т. А (рис.7.7). Видно, что элементарный параллелепипед, выделенный вокруг т. А, находится при плоском напряженном состоянии. Поэтому для проверки прочности применим одну из гипотез прочности.
Рассмотрим напряженное состояние в т. А (рис.7.7). Видно, что элементарный параллелепипед, выделенный вокруг т. А, находится при плоском напряженном состоянии. Поэтому для проверки прочности применим одну из гипотез прочности.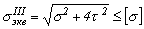 .
. ,
, 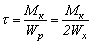 , получим условие прочности вала
, получим условие прочности вала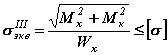 .
.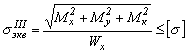 .
. ,
,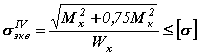 .
.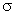 =
=  ,
, 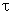 =
=  .
.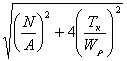
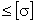 (2.30)
(2.30)



