Исследование свойств параболы1) Вершина параболы: Уравнению (15) удовлетворяют числа 2) Симметрия параболы: Пусть 3) Эксцентриситет параболы: Определение 4.2. Эксцентриситетом параболы называется число
4) Касательная параболы: Касательная к параболе в точке касания
Чертеж 29. 5) Фокус параболы: Если уравнение параболы имеет вид Если уравнение параболы имеет вид 6) Диаметр параболы: Если парабола задана уравнением 7) Уравнения директрис параболы: Если уравнение параболы имеет вид Чтобы обобщить работу по теории линий второго порядка в элементарной математике и для удобства использования информации о линиях при решении задач, заключим все данные о линиях второго порядка в таблицу № 1.
Таблица №1.
|
и 
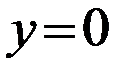, следовательно, парабола проходит через начало координат.[1.c.109-110]
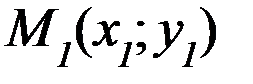принадлежит параболе, т.е. 
верное равенство. Точка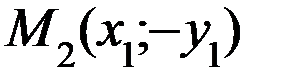 
симметрична точке 
относительно оси 
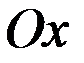, следовательно, парабола симметрична относительно оси абсцисс. [1.С.110]
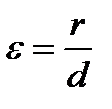, равное единице.
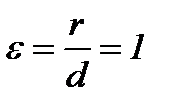, так как по определению параболы 
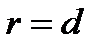.[1.С.110-111]
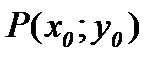определяется уравнением
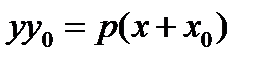, где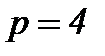 
(чертеж 29.)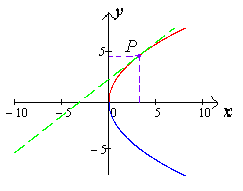
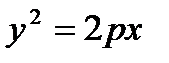, то её фокус имеет координаты 
.
, то её фокус будет иметь координаты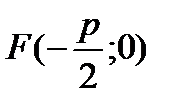 
.
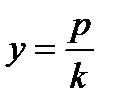,где k угловой коэффициент.
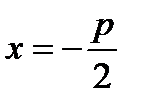. Если уравнение параболы имеет вид 
