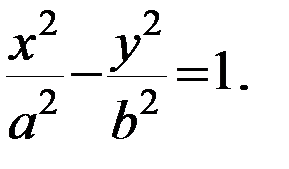Исследование свойств эллипса по его уравнению
1) Пересечение эллипса с осями координат: Ø Найдем точки пересечения эллипса с осью ОХ: Пусть y=0, тогда уравнение эллипса имеет вид: Отсюда следует, что точки (-a,0),(a,0) являются точками пересечения с осью ОХ. Ø Найдем точки пересечения эллипса с осью ОУ: Пусть х=0,отсюда имеем: Следовательно, точки (-b,0),(b,0)являются точками пересечения с осью ОУ. Отсюда заключаем, что границы эллипса Чертеж 9. Расстояние |A1A2| = 2a называется большой (фокальной) осью эллипса, расстояние |B1B2| = 2b называется малой осью эллипса. Расстояния от начала координат до вершин A2(a, 0), B2(0, b) называются соответственно большой и малой полуосями эллипса. Вывод: Таким образом, заключаем, что эллипс вписан в прямоугольник с размерами 2a, 2b (чертеж 10.).
Чертеж 10. 2) Симметрия эллипса относительно координатных осей OX и OY: Пусть Точка
Следовательно, Точка Точка 2) Фокусы эллипса: Пусть фокусы эллипса лежат на оси ОX. Межфокусное расстояние эллипса равно
4) Эксцентриситет эллипса: Определение 2.2. Эксцентриситетом эллипса
Так как Если
Чертеж 11. 5) Диаметры эллипса: Всякая хорда, проходящая через центр эллипса, называется диаметром эллипса. В частности, диаметрами эллипса является его большая ось
Чертеж 12. 6) Касательная к эллипсу: Уравнение касательной к эллипсу
Чертеж 13. 7) Частный случай эллипса - окружность:
8) Взаимное расположение точек и эллипса:
Если Если 9) Уравнения директрис эллипса: Пусть эллипс задан уравнением
ГИПЕРБОЛА Определение 3.1. Гипербола - множество точек плоскости, модуль разности расстояний от которых до двух данных точек Общий вид уравнения
|


 , следовательно
, следовательно  .
.
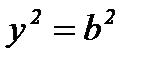 , отсюда
, отсюда  .
. , отображающие его схематичное построение. (чертеж 9.) [1.С. 105]
, отображающие его схематичное построение. (чертеж 9.) [1.С. 105]
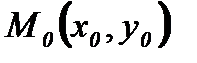 принадлежит эллипсу, т. е
принадлежит эллипсу, т. е  - верное равенство.
- верное равенство. симметрична точке
симметрична точке  относительно оси ОХ
относительно оси ОХ
 - верное равенство.
- верное равенство. принадлежит эллипсу, отсюда заключаем, что эллипс симметричен относительно ОХ
принадлежит эллипсу, отсюда заключаем, что эллипс симметричен относительно ОХ симметрична точке
симметрична точке  симметрична точке
симметрична точке  причем
причем  . Заметим, что
. Заметим, что 




 . [1.С.106]
. [1.С.106] называют отношение межфокусного расстояния 2 с к длине большой оси 2 а.
называют отношение межфокусного расстояния 2 с к длине большой оси 2 а. .
. , следовательно,
, следовательно,  .
. стремится к нулю при постоянном значении
стремится к нулю при постоянном значении  , то
, то  стремится к нулю. При этом величина
стремится к нулю. При этом величина 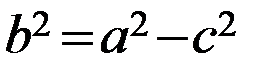 стремится к
стремится к  . В предельном случаи уравнение эллипса принимает вид:
. В предельном случаи уравнение эллипса принимает вид:  . Это уравнение окружности. Если
. Это уравнение окружности. Если  , то
, то  . При этом малая ось эллипса неограниченно уменьшается, эллипс стремится к отрезку. (чертеж 11.) [1.С.106]
. При этом малая ось эллипса неограниченно уменьшается, эллипс стремится к отрезку. (чертеж 11.) [1.С.106]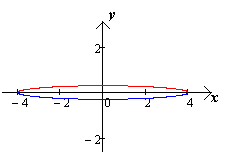
 и малая ось
и малая ось  . Всякий диаметр эллипса, не являющийся его осью, больше малой оси, но меньше большой оси (чертеж 12.). [1.С.106-107]
. Всякий диаметр эллипса, не являющийся его осью, больше малой оси, но меньше большой оси (чертеж 12.). [1.С.106-107]
 где
где  - координаты точки касания и
- координаты точки касания и  соответственно большая и меньшая полуоси эллипса (чертеж 13.).
соответственно большая и меньшая полуоси эллипса (чертеж 13.).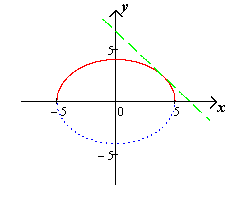


 , где
, где 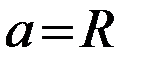 окружности.
окружности.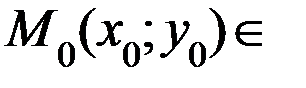 эллипсу, если
эллипсу, если  верное равенство,
верное равенство, то
то  лежит внутри эллипса,
лежит внутри эллипса,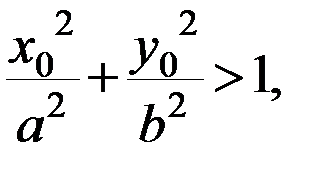 то
то 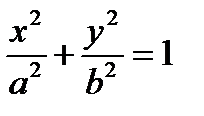 и если при этом
и если при этом  , то
, то  и
и  уравнения директрис эллипса, если
уравнения директрис эллипса, если  , то директрисы определяются уравнениями
, то директрисы определяются уравнениями  .
.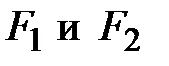 этой плоскости, называемых фокусами гиперболы, есть заданная постоянная величина
этой плоскости, называемых фокусами гиперболы, есть заданная постоянная величина  меньшая, чем расстояние между фокусами
меньшая, чем расстояние между фокусами  [8.С.510]
[8.С.510]