Различные случаи положения прямой линии в пространстве

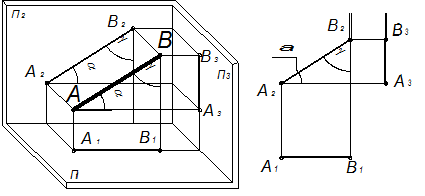
· Горизонтальная прямая или прямая горизонтального уровня – это прямая, параллельная горизонтальной плоскости проекций П₁ (рис. 16). Проецирующая ее на П₂ и П₃ плоскость параллельна П₁, поэтому фронтальная и профильная проекции прямой горизонтальны, а на П₁ она проецируется в натуральную величину (Н.В.). На П₁ также в натуральную величину видны углы β и γ ее наклона к плоскостям П₂ и П₃ соответственно (рис. 17).

Рис. 16 Рис. 17

· Фронтальная прямая или прямая фронтального уровня – это прямая, параллельная фронтальной плоскости проекций П₂ (рис. 18). Плоскость, проецирующая ее на П₁ и П₃, параллельны П₂, поэтому ее горизонтальна проекция на эпюре располагается горизонтально, профильная – вертикально, а на П₂ прямая проецируется в натуральную величину (рис. 19). На П₂ в натуральную величину видны углы α и γ наклона прямой к плоскостям П₁ и П₃.

Рис. 18 Рис. 19

· Профильная прямая или прямая профильного уровня – это прямая, параллельная профильной плоскости проекций (рис. 20). Плоскость, проецирующая ее на плоскости П₁ и П₂, параллельна П₃, поэтому ее фронтальная и горизонтальная проекции на эпюре располагаются вертикально (на одной вертикальной линии проекционной связи), а на профильную плоскость проекций ее отрезки проецируются в натуральную величину (рис. 21). На профильную плоскость проекций в Н.В. проецируются углы α и β наклона прямой к плоскостям проекций П₁ и П₂ соответственно.

Рис. 20 Рис. 21

Для профильной прямой характерны некоторые особенности задания на эпюре.

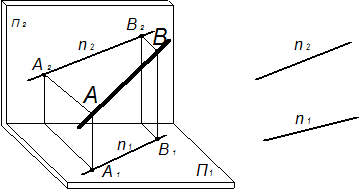
Рис. 22 Рис. 23 Рис. 24

Определяют ли в пространстве прямую m две проекции, заданные на эпюре (рис.22)? Нет. Эпюру (рис. 22) соответствуют в пространстве множество прямых (рис. 23). Следовательно, для профильной прямой недостаточно задания на эпюре фронтальной и горизонтальной проекций в виде неограниченных прямых.

Однако, стоит нам ограничить эту прямую отрезком АВ и обозначить его на эпюре (рис. 24), как оказывается заданной в пространстве вполне определенная прямая (рис. 25). Кроме задания профильной прямой двумя проекциями отрезка (рис. 24), можно задать профильную прямую a тремя проекциями луча или неограниченной прямой (рис. 26).

Рис. 25 Рис. 26

§ Горизонтально-проецирующая прямая или прямая двойного уровня – это прямая, перпендикулярная к горизонтальной плоскости проекций П₁ (рис. 27). При этом она параллельна одновременно двум оставшимся плоскостям проекций П₂ и П₃, и поэтому называется еще прямой двойного уровня. Горизонтальная ее проекция – точка, а фронтальная и профильная – вертикальные прямые (рис. 28). На фронтальную и профильную проекций она проецируется в натуральную величину.

Рис. 27 Рис. 28

§ Фронтально-проецирующая прямая или прямая двойного уровня это прямая, перпендикулярная к фронтальной плоскости проекций П₂ и одновременно параллельная плоскостям П₁ и П₃. Эпюр этой прямой приведен на рис. 29. Наглядное изображение ее предлагается построить студенту самому. На какие плоскости проекций она проецируется в натуральную величину?

Рис. 29 Рис. 30

§ Профильно-проецирующая прямая или прямая двойного уровня – это прямая, перпендикулярная к профильной плоскости проекций П₃ и параллельная П₁ и П₂. Эпюр ее приведен на рис. 30. Постройте ее наглядное изображение. На какие плоскости проекций она проецируется в натуральную величину?

§ Прямая общего положения – это прямая, не параллельная и не перпендикулярная ни к одной из плоскостей проекций (рис. 14, 15). В этом случае проекции прямой располагаются под произвольными углами к оси Х (рис. 31 и 32).

Рис. 31

Рис. 32

На рис. 31 изображена нисходящая прямая. Эта прямая, которая понижается по мере удаления от наблюдателя. На рис. 32 – восходящая прямая, она повышается по мере удаления от наблюдателя. Сравним эпюры этих прямых. Замечаем, что у восходящей прямой проекции наклонены к линиям проекционной связи в одну и ту же сторону, а у нисходящей – в разные. Назовем этот признак ориентацией и скажем, что проекции восходящей прямой ориентированы одинаково, а нисходящей – противоположно.

Поскольку проекции прямой общего положения получаются искаженными (уменьшенными) в сравнении с натуральной длиной ее, то возникает вопрос определения натуральной величины (Н.В.) отрезка прямой общего положения и углов ее наклона к плоскости проекций.