Методом прямоугольного треугольника
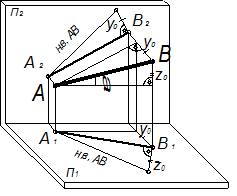
Рассмотрим схему проецирования прямой на плоскости П1 и П2 (рис. 15 и 33). АВ – прямая в пространстве, А1В1 – горизонтальная проекция прямой на плоскости П1. Через точку А проведем прямую, параллельную А1В1. Получим прямоугольный треугольник, в котором один катет равен А1В1, второй катет – разности аппликат концов отрезка (т.е. представляет собой относительную аппликату z0 точки В по точке А), а гипотенуза есть сам отрезок АВ. Угол α есть угол наклона прямой АВ к горизонтальной плоскости проекций. Сдвинем этот треугольник до совмещения с проекцией А1В1, а затем повернем его вокруг А1В1 до наложения на плоскость П2. В наложенном на плоскость треугольнике гипотенуза уже не является пространственной прямой, но по величине ей равна. Перенесем полученное построение на эпюр (рис. 34). На А1В1, как на катете, строится прямоугольный треугольник, второй катет которого является z0 и измеряется на фронтальной плоскости проекций. Тогда гипотенуза равна натуральной величине (Н.В.) отрезка АВ. Угол между натуральной величиной и горизонтальной проекцией А1В1 определяет угол α наклона прямой АВ к П1. Совершенно аналогичные построения можно выполнить для определения угла β наклона прямой АВ к плоскости П2. Для этого на рис. 33 через точку А проведем прямую, параллельную фронтальной проекции отрезка А2В2. Полученный прямоугольный треугольник, вторым катетом которого является разность ординат концов отрезка y0, переместим к А2В2, а затем повернем его вокруг А2В2 до наложения на плоскость П1. Полученное построение выполнено на эпюре рис. 34. Величина у0 = у – уА и замерена при горизонтальной проекции отрезка. Между Н.В. отрезка АВ и его фронтальной проекцией получается угол β наклона прямой АВ к фронтальной плоскости проекций.
Рис. 33 Рис. 34
Итак: натуральная величина отрезка равна гипотенузе прямоугольного треугольника, один катет которого есть любая проекция отрезка, а второй равен разности расстояний концов отрезка от плоскости проекций, на которой выбран первый катет.
|