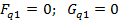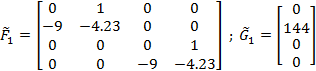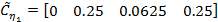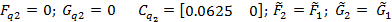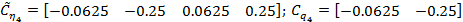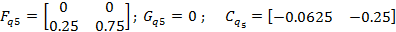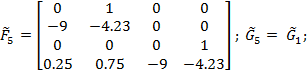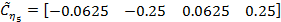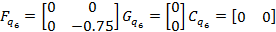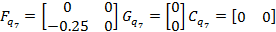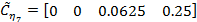Задание 2 – Построение МТЧ ДОУ к вариации интервала дискретности
Интервал дискретности В качестве метода перехода к дискретному векторно-матричному описанию ВСВ описанию ДОУ используется метод замены производной отношением конечных малых.
Переход к дискретному описанию ОУ осуществляется по формулам:
Где
откуда при
Построение модели траекторной чувствительности к вариации интервала дискретности:
Построение агрегированного ОУ:
Матрицы агрегированной системы имеют представление:
Получим:
Задание 3 – Построение МТЧ спроектированной непрерывной замкнутой системы (ЗС)
Дано:
Закон управления:
, где
образованной объединением НОУ и ЗУ, с помощью: -матрицы kg прямой связи по входу g(t) равенство входа g(t) и выхода y(t) в неподвижном состоянии при номинальных значениях параметров; - матрицы k обратной связи по состоянию x(t) при номинальных значениях параметров распределение мод. При произвольном значении
Найдем матрицы:
Для распределение мод Баттерворта с характеристической частотой
Сконструируем матрицу
Закон управления примет вид:
Найдем передаточную функцию замкнутой системы управления:
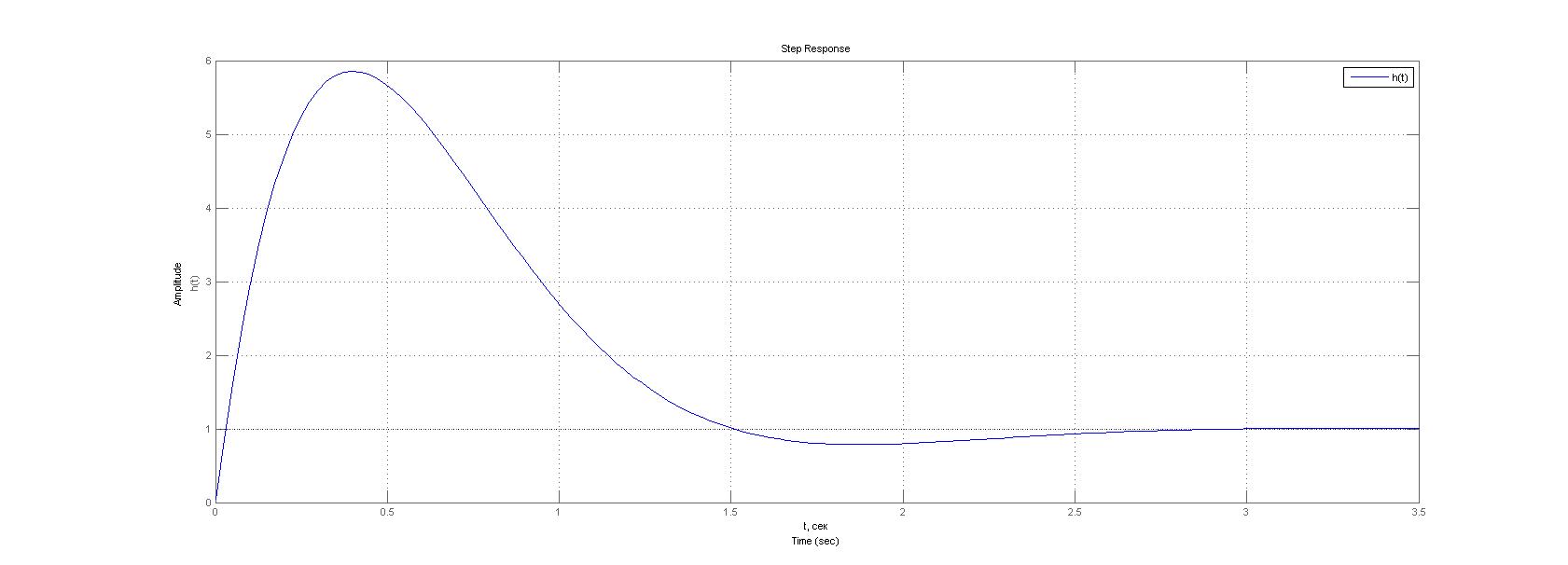
Переходная функция такой системы представлена на рисунке 3.1
Рисунок 3.1 – Переходная функция номинальной СУ. tп=1.36 сек; hmax=5.86; h∞=1; Построение семейства моделей траекторной чувствительности:
Получим матрицы агрегированной системы
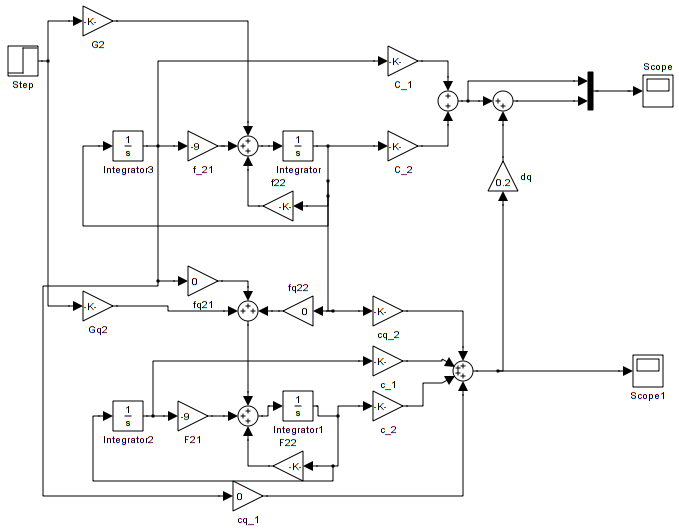
На рисунке 3.2 представлена структурная схема агрегированной системы: номинального объекта управления и модели траекторной чувствительности к вариации одного из параметров.
Рис. 3.2 – Структурная схема агрегированной системы Построим графики переходных функций возмущенных по одному из параметров и сравним с графиком переходной функции номинальной системы.
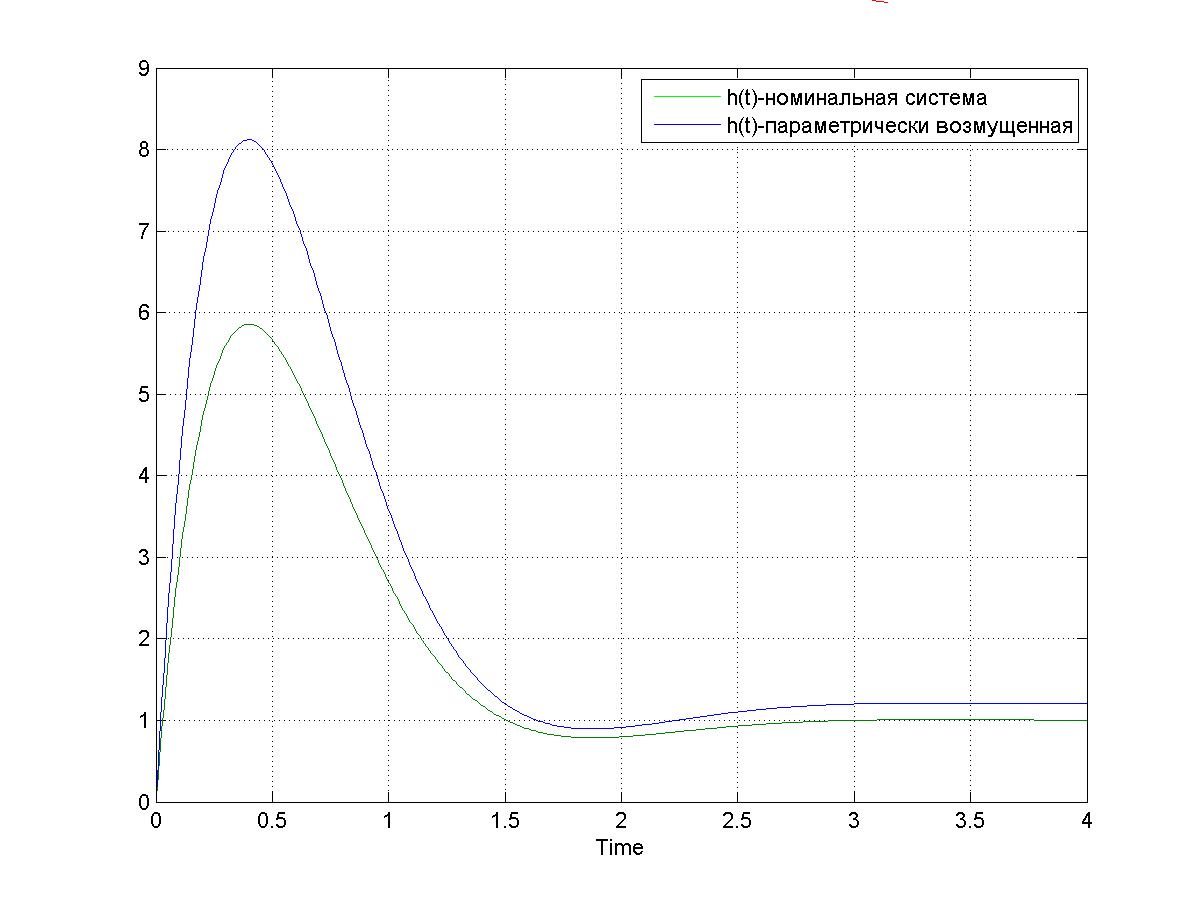
При j=1, 𝛥q=0.2 переходная функция будет иметь вид:
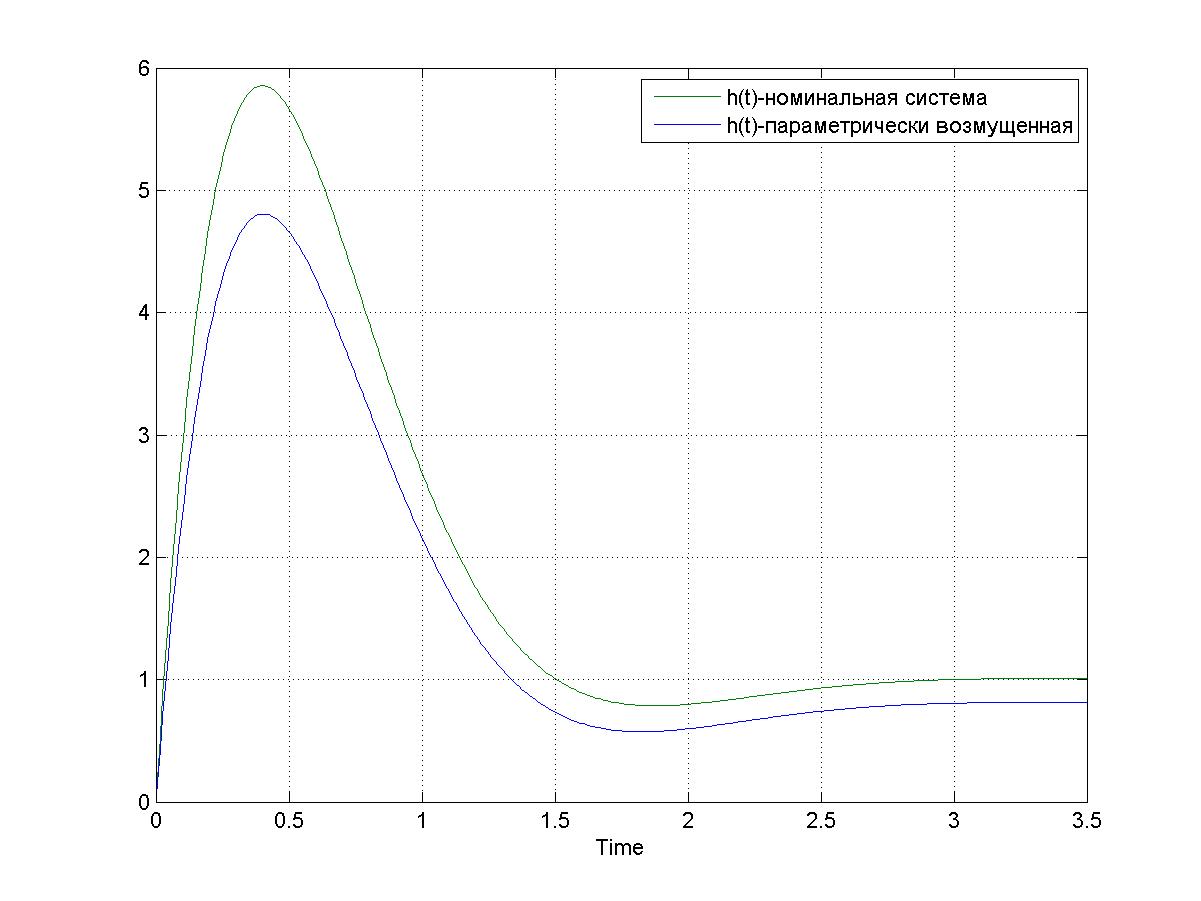
Рис. 3.3. – Переходная функция номинальной и возмущенной системы по параметру q1. tп=1.4; hmax=8.1; h∞=1.2; При j=2, 𝛥q=0.2 переходная функция будет иметь вид:
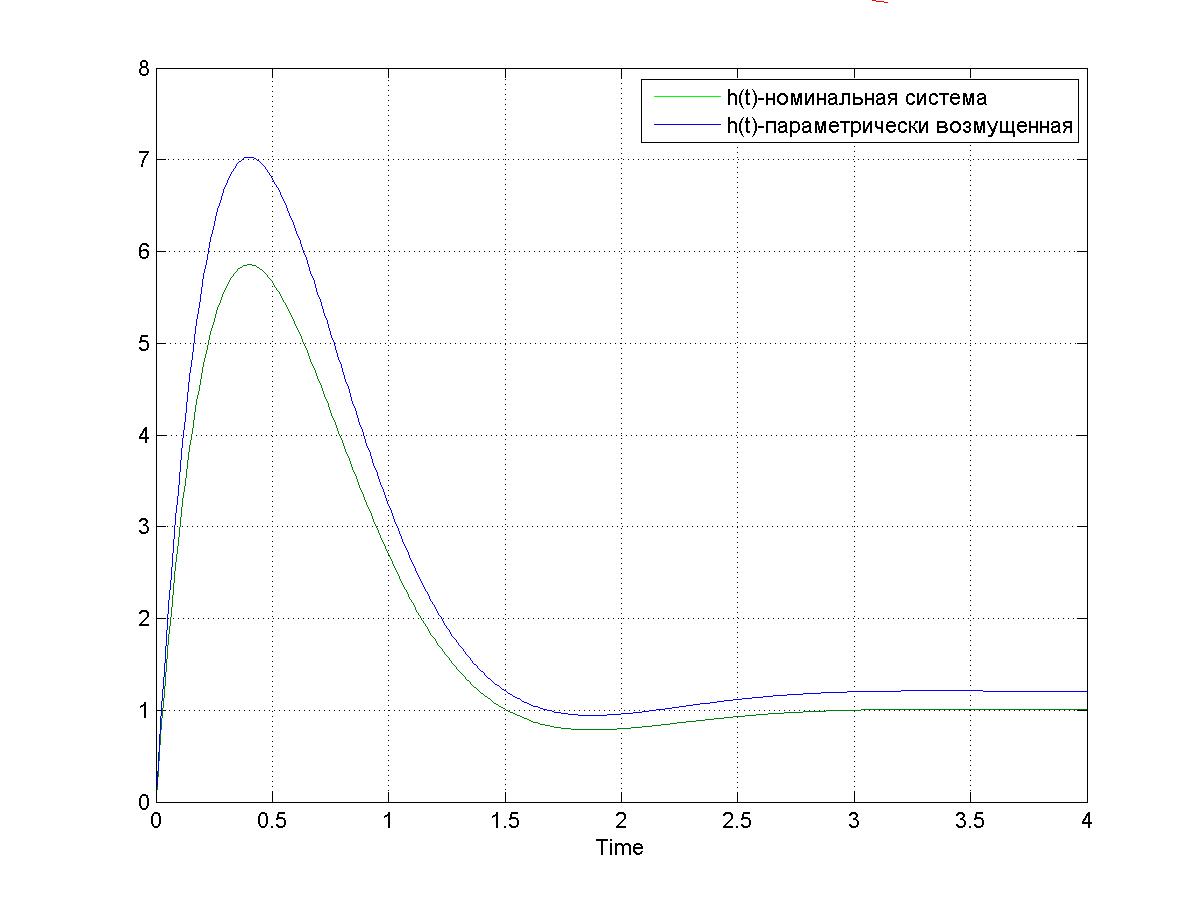
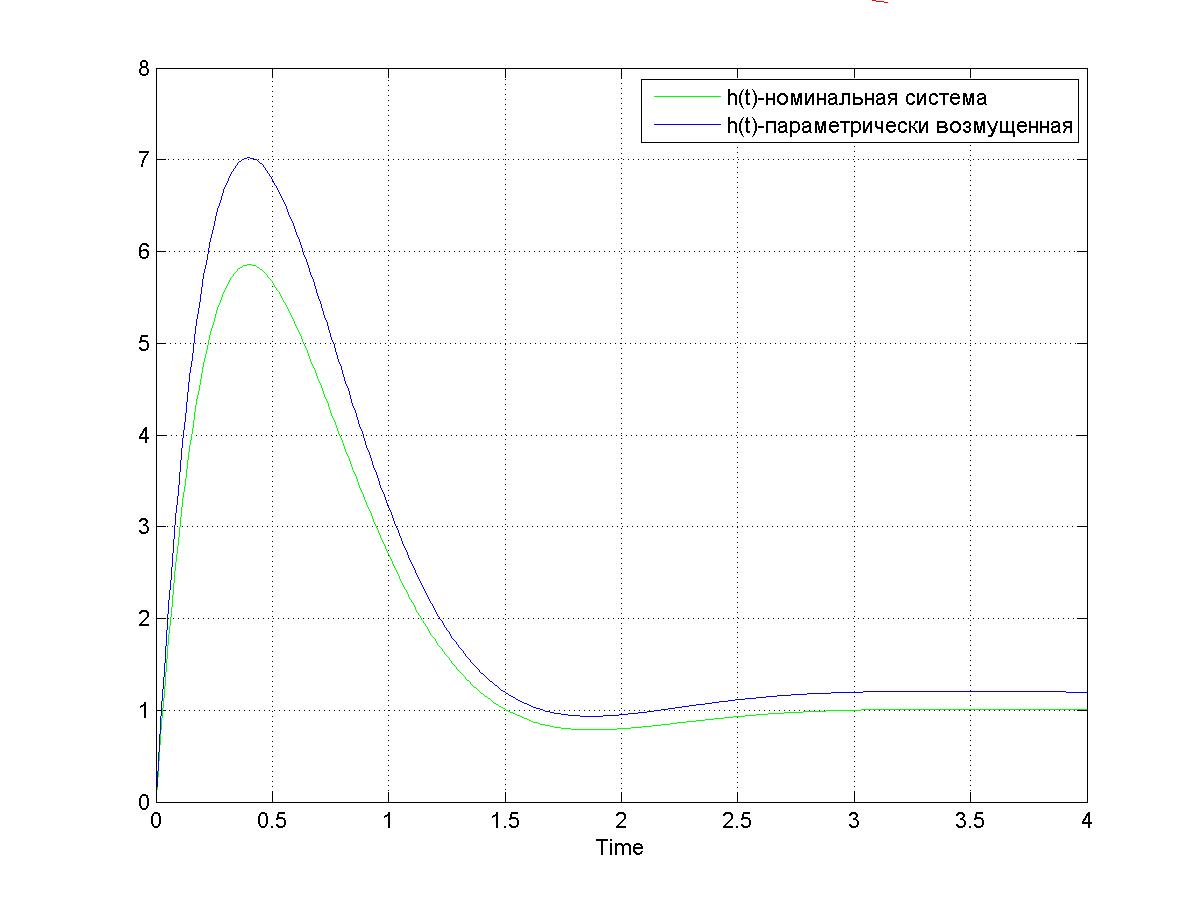
Рис. 3.4. – Переходная функция номинальной и возмущенной системы по параметру q2, tп=1.36; hmax=7.01; h∞=1.2;
При j=4, 𝛥q=0.2 переходная функция будет иметь вид:
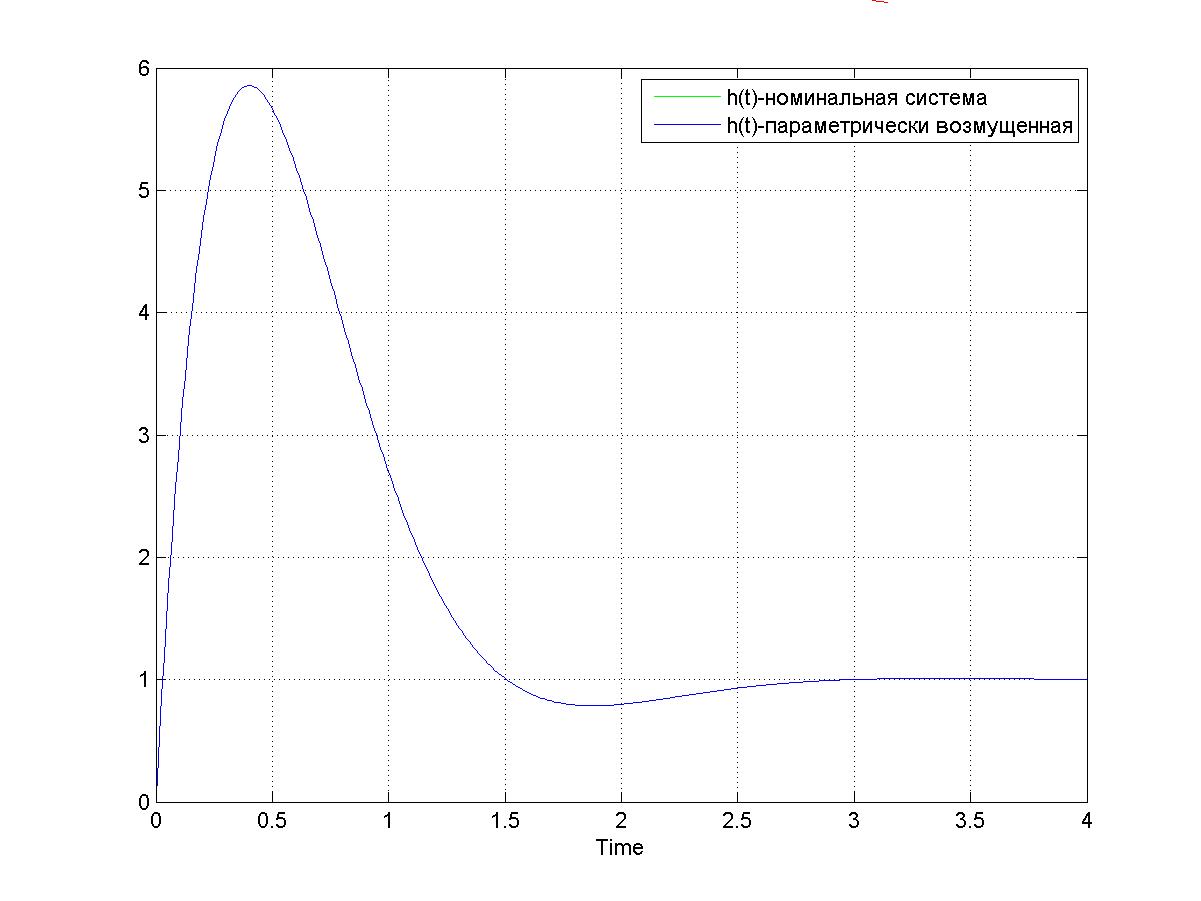
Рисунок 3.5. Переходная функция номинальной и возмущенной системы по параметру q4 t П =1.36; hmax=5.86; h∞=1. При j=5, 𝛥q=0.2 переходная функция будет иметь вид:
Рисунок 3.6 – Переходная функция номинальной и возмущенной системы по параметру q5 t П =1.36; hmax=6; h∞=0.7.
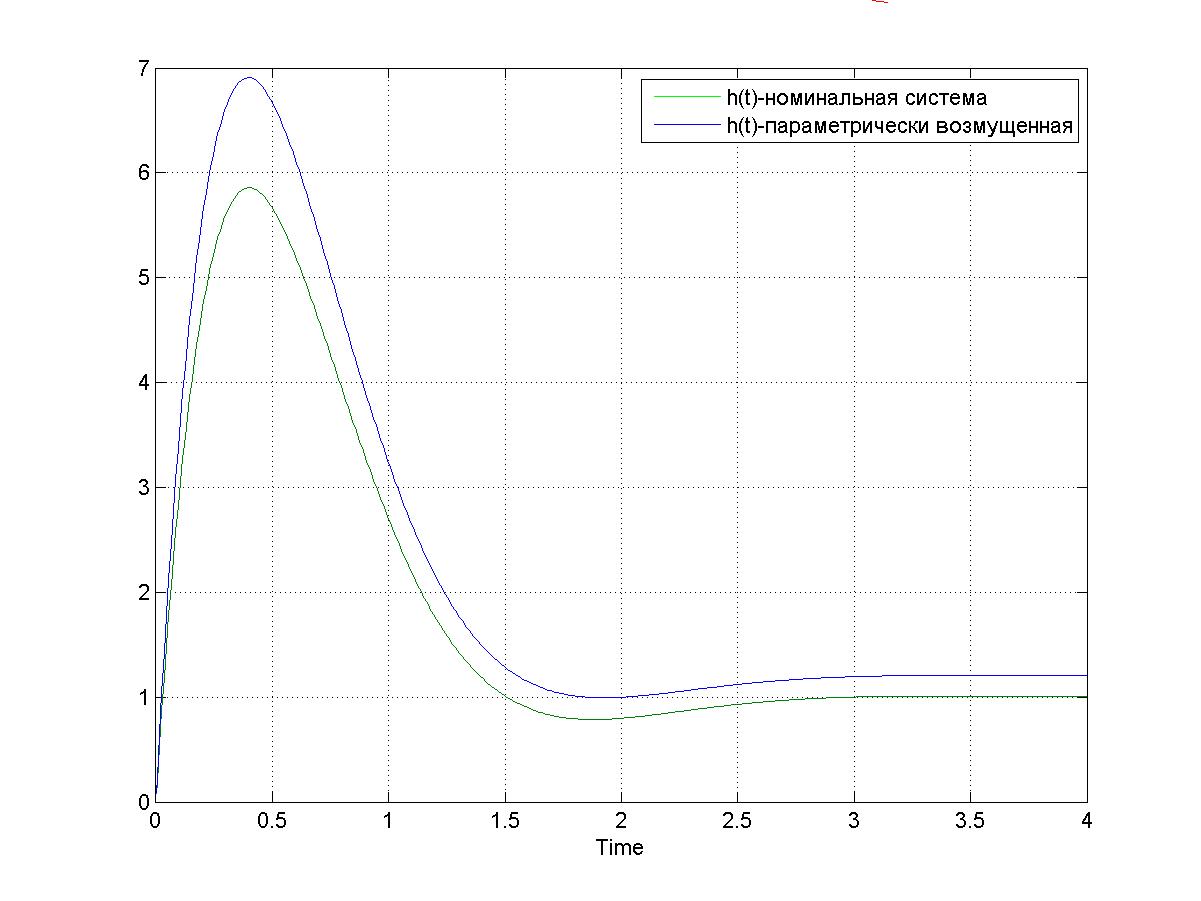
При j=6, 𝛥q=0.2 переходная функция будет иметь вид:
Рисунок 3.7 – Переходная функция номинальной и возмущенной системы по параметру q6 tп=1.36 hmax=6.9 h∞=1.2 При j=7, 𝛥q=0.2 переходная функция будет иметь вид:
Рисунок 3.8 – Переходная функция номинальной и возмущенной системы по параметру q7 tп=1.36 hmax=7.02 h∞=1.2
ранжируем параметры qj по степени влияния на качество замкнутой системы q1>q7>q2>q6>q5>q4. Для 𝛥q=-0.2 получим следующие результаты: При j=1, 𝛥q=-0.2 переходная функция будет иметь вид:
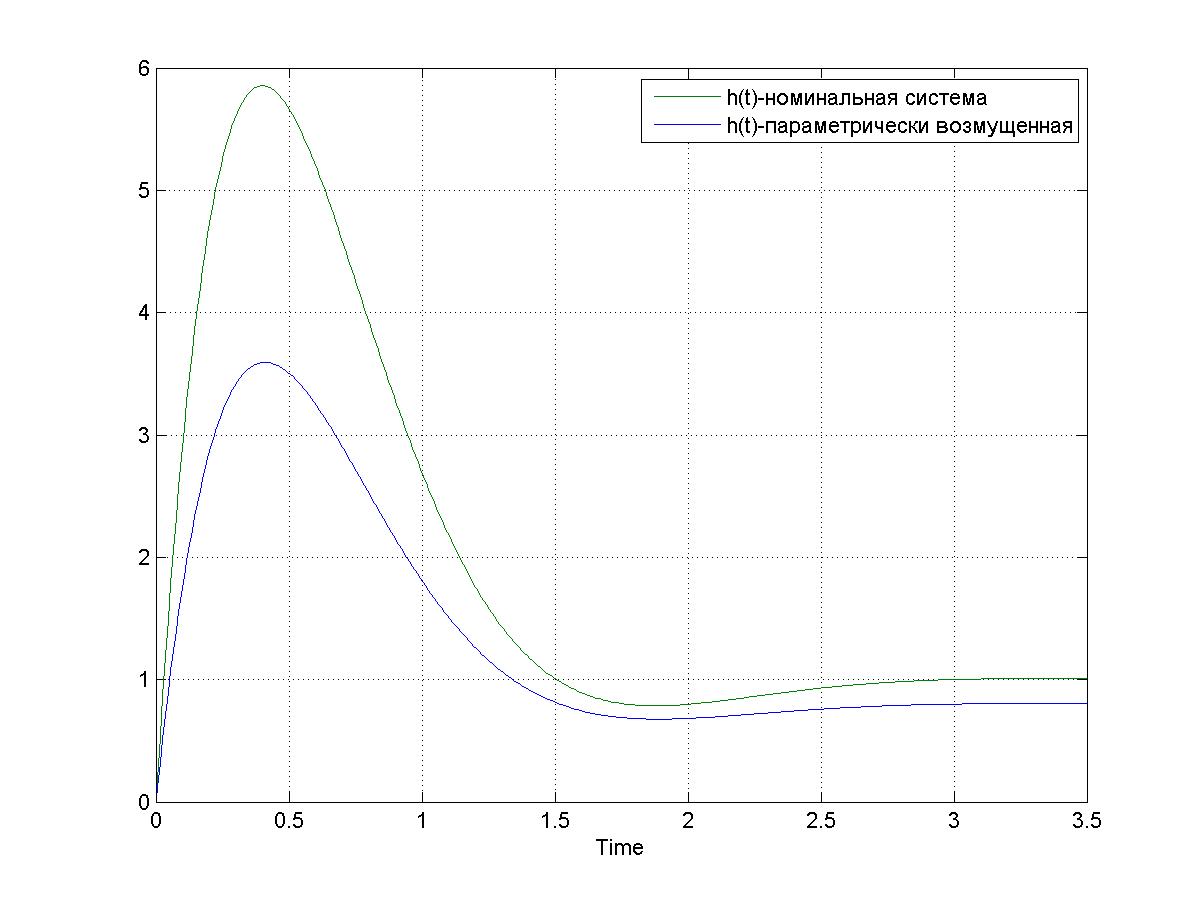
Рис. 3.3. – Переходная функция номинальной и возмущенной системы по параметру q1. tп=1.1; hmax=3.6; h∞=0.8;
При j=2, 𝛥q=-0.2 переходная функция будет иметь вид:
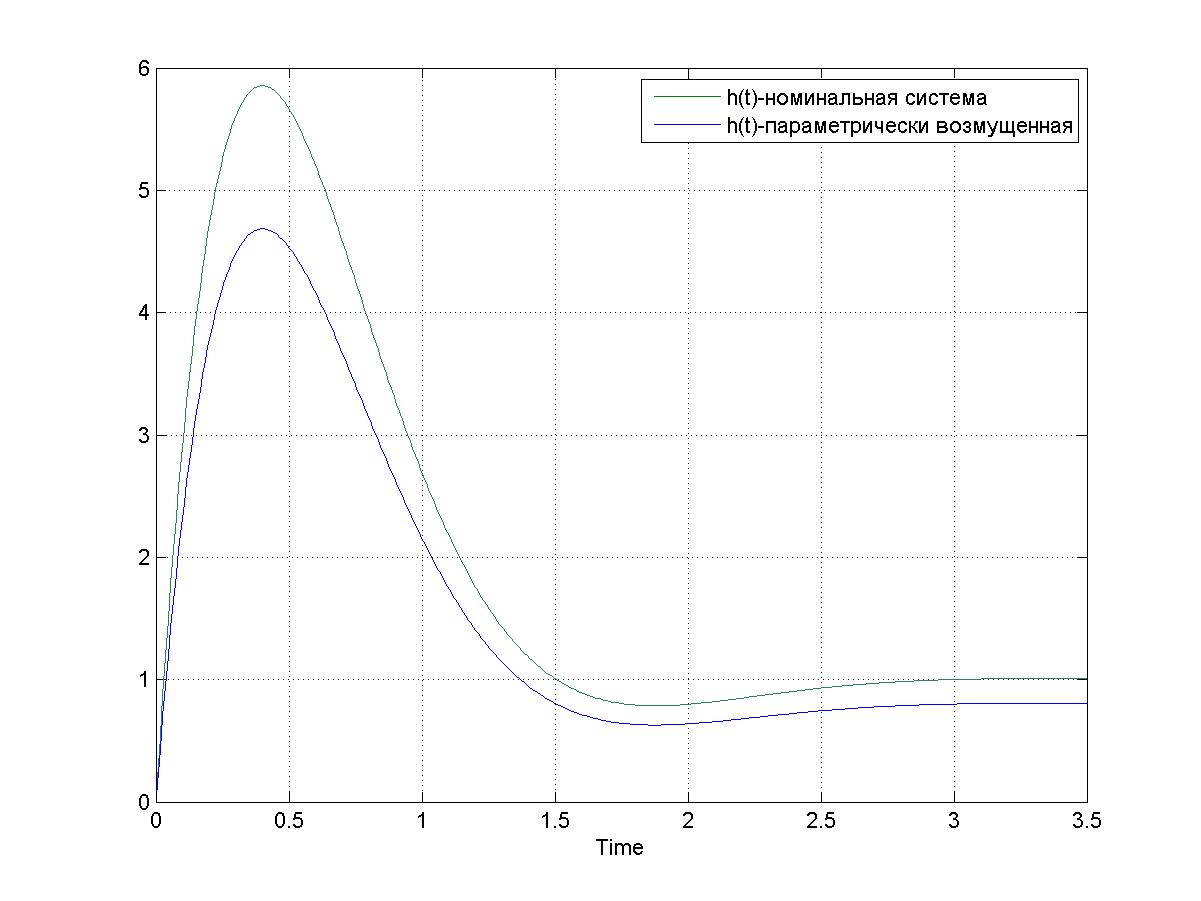
Рис. 3.4. – Переходная функция номинальной и возмущенной системы по параметру q2, tп=1.2; hmax=4.7; h∞=0.8; При j=4, 𝛥q=-0.2 переходная функция будет иметь вид:
Рисунок 3.5. Переходная функция номинальной и возмущенной системы по параметру q4 t П =1.2; hmax=4.7; h∞=0.8.
При j=5, 𝛥q=-0.2 переходная функция будет иметь вид:
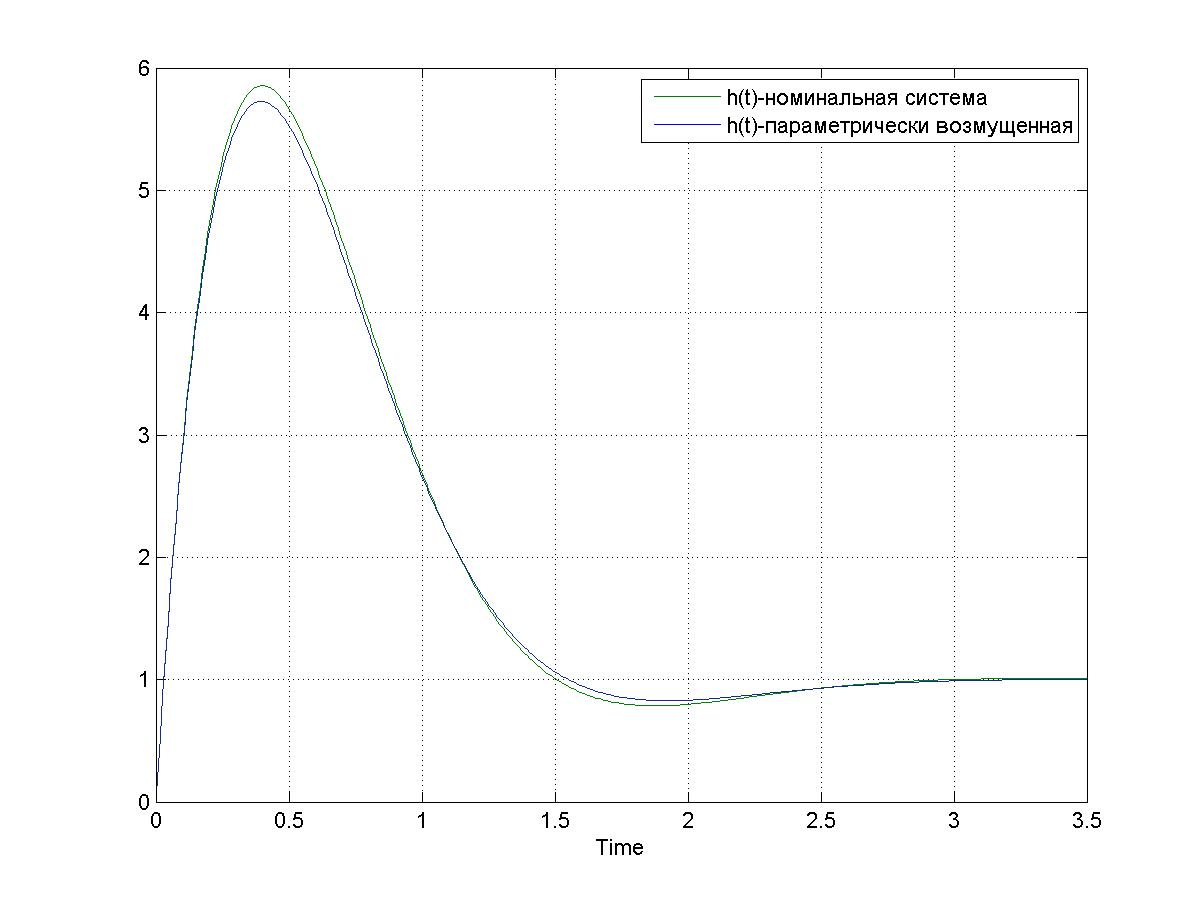
Рисунок 3.6 – Переходная функция номинальной и возмущенной системы по параметру q5 t П =1.36; hmax=5.72; h∞=1.
При j=6, 𝛥q=-0.2 переходная функция будет иметь вид:
Рисунок 3.7 – Переходная функция номинальной и возмущенной системы по параметру q6 tп=1.2 hmax=4.8 h∞=1.2 При j=7, 𝛥q=-0.2 переходная функция будет иметь вид:
Рисунок 3.8 – Переходная функция номинальной и возмущенной системы по параметру q7 tп=1.2 hmax=4.8 h∞=0.8
ранжируем параметры qj по степени влияния на качество замкнутой системы q1>q7=q2>q6=q4>q5.
|
.
, 
, 
,
, 
:
.
;
; 
;
;
, 
;
, 
.
, 
, 
.
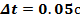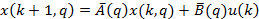
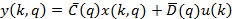
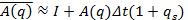
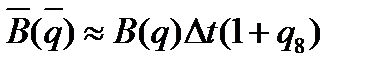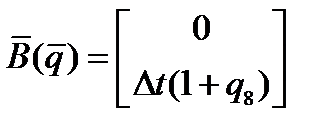
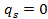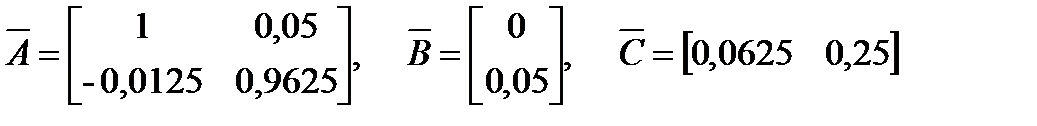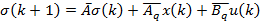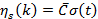
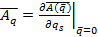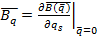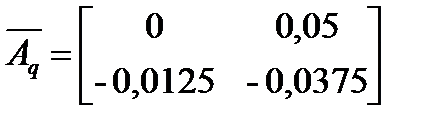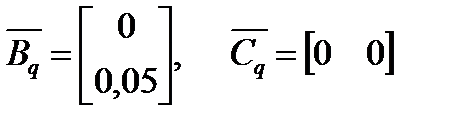
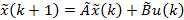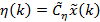
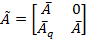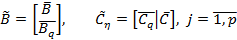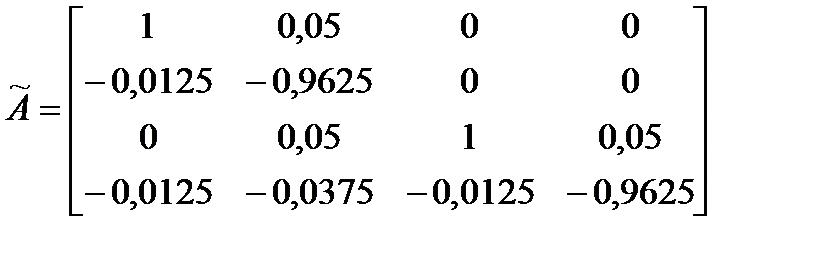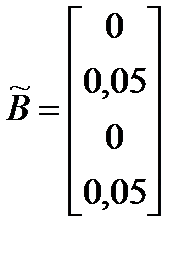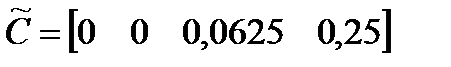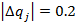
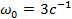
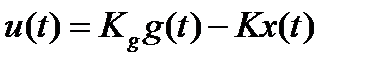должен доставлять системе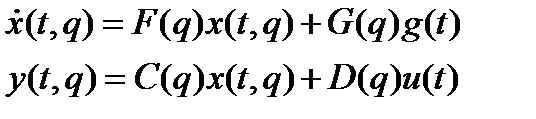
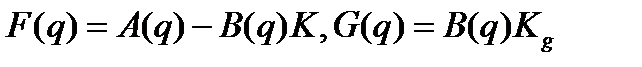
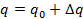векторе параметров исследуемая система имеет векторно-матричное представление: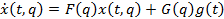
;
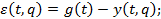
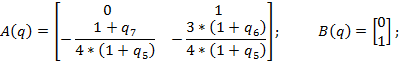
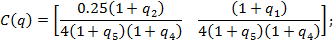
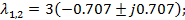
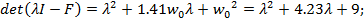
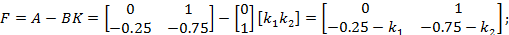
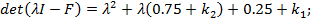
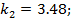
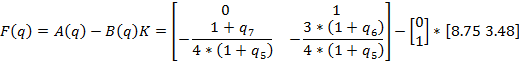
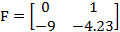
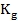прямой связи по внешнему задающему воздействию
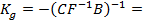144;
;
;
; 
;
;
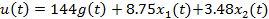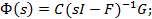
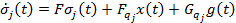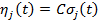
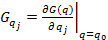