Задание 6 – Исследование робастности полученной ЗС методом В.Л.Харитонова
Чтобы интервальный характеристический полином был гурвицевым, необходимо и достаточно, чтобы были гурвицевыми четыре его угловые версии.
Интервальная матрица состояния спроектированной ЗС имеет вид:
Матрица
где
Полиномы В.Л.Харитонова в этом случае записываются в форме:
В силу положительности коэффициентов, все полиномы Л.В.Харитонова являются гурвицевыми, а, следовательно, гурвицевым является и ИХП
Задание 7 – Синтез параметрически инвариантной системы
1. Зададим ВМО ВСВ НОУ в каноническом управляемом базисе:
граничные (угловые) значения:
2. Построение факторизованного представления матричного компонента
где каждый матричный компонент полной вариации удовлетворяет условию
Подставив в уравнения системы, получим:
Введем новые обозначения:
Подставим введенные обозначения в уравнения системы:
3. Сформируем требования к качеству процессов по выходным переменным
где
выход
Представим сформированные требования в виде желаемой структуры мод
Определяем свободные параметры условия принадлежности:
откуда следует, что
Таким образом спектр собственных чисел матрицы
Проверка условия принадлежности к ядру матрицы:
Проверим выполнение условия
4. Решение уравнений Сильвестра
Сконструируем матрицу
где
Уравнение Сильвестра в силу специфики задачи представим в факторизованном по алгебраическому и геометрическому спектрам матрицы
Представим это выражение в виде двух уравнений Сильвестра:
где
Найдем решение этих уравнений относительно матриц
5. Вычислим матрицу отрицательной обратной связи
6. Сконструируем матрицу
Построим реализационную версию закона управления в виде
где
Проведём проверку эффективности спроектированного неадаптивного закона управления на предмет удовлетворения техническим требованиям показателей качества по выходу
Рисунок 7.1 – Схема моделирования номинальной системы
Рисунок 7.2 – Схема моделирования возмущенной системы
Рисунок 7.3 – Схема моделирования возмущенной системы

Рис. 7.2. Графики переходных процессов в номинальной и возмущенной системах/
отклонение при минимальном значении варьируемых параметров отклонение при максимальном значении варьируемых параметров Заключение В данной работе было проведено исследование параметрической чувствительности объектов и систем, и осуществлен синтез не адаптивного алгоритма обеспечивающего необходимую робастность динамических показателей системы. В частности, была построена модель траекторной чувствительности НОУ, параметры qj проранжированы с использованием матрицы управляемости агрегированной системы. Осуществлено исследование модели траекторной чувствительности дискретного объекта к вариации интервала дискретности. Построена МТЧ непрерывной замкнутой системы и синтезирован закон управления доставляющей системе желаемые динамические и точностные свойства. Оценены наиболее и наименее благоприятные распределения параметров. Произведен синтез замкнутой системы заданной интервальными элементами методом модального управления. И проведено исследование робастности системы методом В.Л.Харитонова. Также был синтезирован закон управления, обеспечивающий системе помимо желаемых точностных и динамических показателей параметрическую инвариантность выходной переменной.
Список литературы 1. Дударенко Н.А., Слита О.В., Ушаков А.В. Математические основы современной теории управления: аппарат метода пространства состояний: учебное пособие. / Под ред. Ушакова А.В. – СПб: СПбГУ ИТМО, 2008. – 323 с. 2. Никифоров В.О., Ушаков А.В. Интеллектуальное управление в условиях неопределенности. – СПб.: СПб ГИТМО (ТУ), 2010.
3. Никифоров В.О. Адаптивное и робастное управление с компенсацией возмущений. – СПб.: Наука, 2003.
|

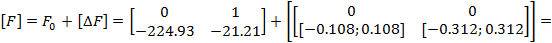

 имеет интервальный характеристический полином (ИХП)
имеет интервальный характеристический полином (ИХП) ,
, ,
,  ,
, 




 . А это, по теореме В.Л.Харитонова, означает, что полученная в пункте 5 замкнутая система устойчива.
. А это, по теореме В.Л.Харитонова, означает, что полученная в пункте 5 замкнутая система устойчива. ,
,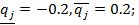


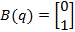

 :
:

 и представим в виде
и представим в виде , с максимальным значением
, с максимальным значением  , равным числу ненулевых элементов
, равным числу ненулевых элементов  .
. ,
, – внешнее параметрическое воздействие
– внешнее параметрическое воздействие

 в переходном и установившемся режимах при задающем внешнем воздействии r wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">
в переходном и установившемся режимах при задающем внешнем воздействии r wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">  номинальной версии проектируемой системы
номинальной версии проектируемой системы ,
, ,
, инвариантен относительно
инвариантен относительно  , так что выполняются соотношения
, так что выполняются соотношения
 , где
, где 

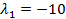 , а
, а  .
. примет вид:
примет вид:

 . Так как условие выполняется, можно решить полную задачу обобщенного модального управления.
. Так как условие выполняется, можно решить полную задачу обобщенного модального управления. отрицательной обратной связи методом обобщенного модального управления, опирающегося на решение матричного уравнения Сильвестра:
отрицательной обратной связи методом обобщенного модального управления, опирающегося на решение матричного уравнения Сильвестра: ,
,

 ,
,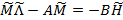 ,
,
 и
и  соответственно:
соответственно:


 прямой связи по внешнему задающему воздействию r wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">
прямой связи по внешнему задающему воздействию r wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 
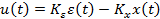 ,
,
 номинальной версии системы, а также наличие у системы параметрической инвариантности.
номинальной версии системы, а также наличие у системы параметрической инвариантности.

 .
.
 .
.
 .
. от номинального значения
от номинального значения  составляет 0.049%.
составляет 0.049%. от номинального значения
от номинального значения 


