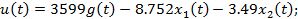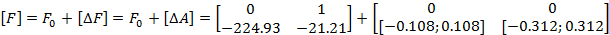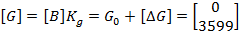Задание 5 – Построение закона управления для объекта, заданного интервальными элементами
Дано ВМО ВСВ НОУ с интервальными матричными компонентами в форме
получаемое с использованием интервальной арифметики на основе интервальной реализации параметров
при следующих граничных (угловых) значениях: t wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/></w:rPr><m:t>j</m:t></m:r></m:sub></m:sSub></m:e></m:bar><m:r><w:rPr><w:rFonts w:ascii="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/></w:rPr><m:t>=0.2 </m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000" wsp:rsidRPr="0022333A"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> Закон управления (ЗУ):
образованной объединением НОУ и ЗУ, с помощью: - матрицы - матрицы
Не больше заданной Методом модального управления, базовый алгоритм которого, опирающийся на решение матричного уравнения Сильвестра и примененный к медианным составляющим интервальных матричных компонентов ВМО ВСВ НОУ, дополняется контролем нормы Формирование ВМО ВСВ интервального ОУ:
Описания объекта в параметрическом виде:
Сформируем матрицу состояний в интервальном виде.
Матрица
Составим таблицу граничных значений матрицы состояния.
Таблица 1- Экстремальные значение параметров матрицы состояния
Граничные значения матрицы
Медианное значение интервальной матрицы находятся как половину суммы угловых значений.
Модальная модель желаемой системы имеет вид:
Матрица
Матрица
Решим задачу медианного МУ с помощью уравнения Сильвестра:
Формирование медианной составляющей
Проверка выполнения условия:
Таким образом, на частоте среза Формирование закона управления:
Закон управления примет вид:
Интервальные матрицы описания системы имеют вид:
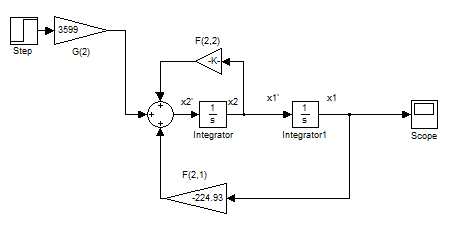
Построим модель полученной системы:
Рисунок 5.1 – Структурная схема синтезированной замкнутой системы
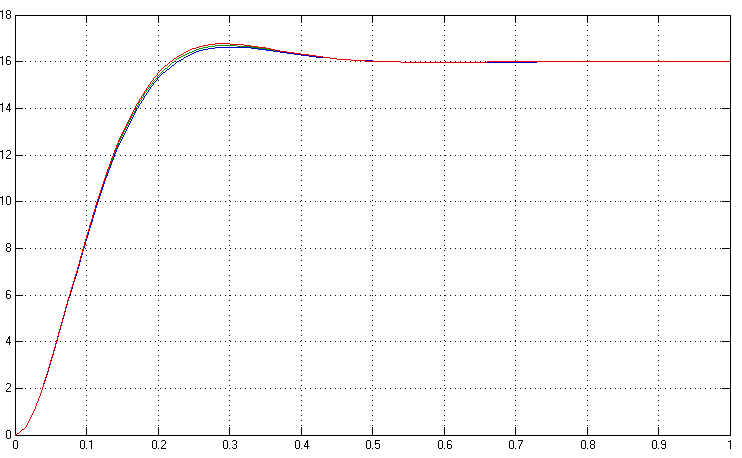
Рисунок 5.2 – Переходная характеристика для медианного(h0(t)) максимального(hmax(t)) и минимального(hmin(t)) набора параметров
|

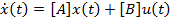
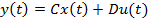
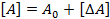 ,
, 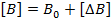
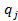 , записываемых в форме
, записываемых в форме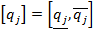
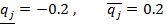
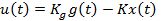 должен доставлять системе с интервальными матричными компонентами.
должен доставлять системе с интервальными матричными компонентами.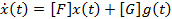
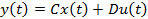
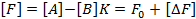
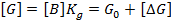
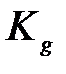 прямой связи по входу
прямой связи по входу 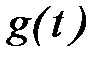 равенство входа
равенство входа 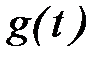 и выхода
и выхода 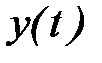 в неподвижном состоянии при медианных значениях параметров;
в неподвижном состоянии при медианных значениях параметров;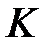 обратной связи по состоянию
обратной связи по состоянию 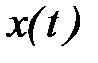 при медианных значениях параметров распределение мод Баттерворта с характеристической частотой
при медианных значениях параметров распределение мод Баттерворта с характеристической частотой 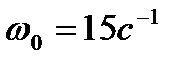 , которая гарантирует достижение оценки относительной интервальности матрицы состояния системы
, которая гарантирует достижение оценки относительной интервальности матрицы состояния системы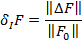
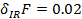 .
.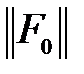 медианной составляющей интервальной матрицы
медианной составляющей интервальной матрицы 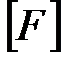 спроектированной системы с последующим вычислением оценки
спроектированной системы с последующим вычислением оценки 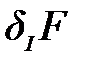 , вычислить матрицы
, вычислить матрицы 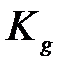 и
и 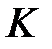 .
.
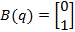

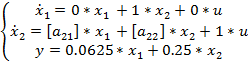
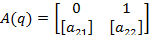
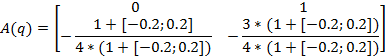
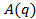 примет вид:
примет вид: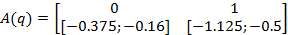

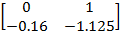
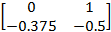
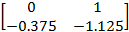
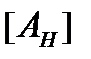 получаются с помощью компоновки экстремальных значений каждой составляющей матрицы
получаются с помощью компоновки экстремальных значений каждой составляющей матрицы  .
.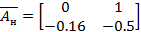 ,
, 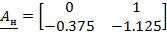
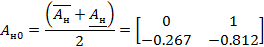
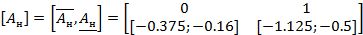
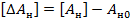
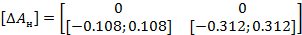
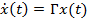
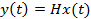
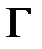 составляется, исходя из требуемого распределения мод
составляется, исходя из требуемого распределения мод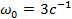 , собственные значения имеют реализацию
, собственные значения имеют реализацию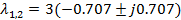
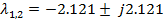
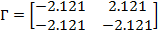
 выбирается из условия полной наблюдаемости пары Г и Н:
выбирается из условия полной наблюдаемости пары Г и Н: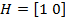
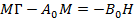
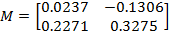
 интервальной матрицы
интервальной матрицы 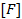 :
: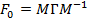 ;
;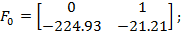
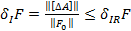 ;
;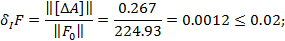
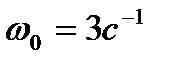 достигается требуемая относительная интервальность матрицы состояния системы.
достигается требуемая относительная интервальность матрицы состояния системы.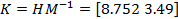 ;
;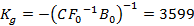 ;
;