Сравнение средних значений в двух группах – Т-критерий Стьюдента
Данный критерий можно применять для сравнения средних значений ТОЛЬКО метрических переменных и ТОЛЬКО в ДВУХ группах (не в трех, четырех, …) В нашем примере метрическими являются переменные: · №3 –Age – возраст · №5 – Stajj – стаж работы · №7 – ProfStress – показатель профессионального стресса · №9 – Maslach_1 – первый показатель методики Маслач · №10 – Maslach_2 – второй показатель методики Маслач · №11 – Maslach_3 – третий показатель методики Маслач Переменная «Пол» делит всех участников на две группы – мужчины и женщины. Переменная «Group» делит всех участников на две группы – экспериментальная группа и контрольная группа. Соответственно, в нашем примере с помощью Т-критерия Стьюдента можно проверить, 1) отличаются ли средние значения перечисленных выше переменных у мужчин и женщин; 2) отличаются ли средние значения перечисленных выше переменных у участников экспериментальной и контрольной группы.
В верхнем меню выберите пункт Statistics – в нём Basic Statistics/Tables.
Далее как на рисунке – t-test, independent, by groups. Это критерий Стьюдента.
Появляется окошко с настройками. Прежде всего, нужно выбрать переменные, для которых хотим провести расчет. Для этого щелкните кнопку Variables как показано на рисунке:
Появляется окно выбора переменных.
Здесь в левой части – Dependent variables – нужно указать те метрические переменные, средние значения которых хотим сравнить. Например, это переменные 3, 5, 7, 9-11 (возраст, стаж, стресс, и т.д.). Можно выбрать переменные из списка или в пустом окне напечатать номера. В правой части – Grouping variable – указываем ОДНУ переменную, которая делит нашу выборку на две группы. Например, можно выбрать переменную 1-Pol, тогда будем сравнивать показатели мужчин и женщин. Либо можно здесь выбрать переменную 2-Group, тогда будем сравнивать экспериментальную и контрольную группы. Если нас интересуют оба варианта, то придется дважды применять Т-критерий. Но за один раз выбирается только одна переменная в правой части окна. Сейчас рассмотрим пример с переменной 1-Pol. Это будет выглядеть так:
Программа возвращает нас в предыдущее окно. Для выполнения расчетов нужно нажать кнопку Summary, одну из двух, они показаны на картинке.
На экране появится еще одно окно – Workbook1. В этот файл программа будет записывать все результаты вычислений.
Рассмотрим подробно полученные результаты.
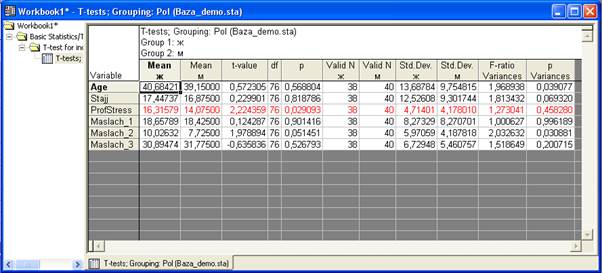
В таблице слева на сером фоне перечислены переменные, средние значения которых мы сравнивали. Столбцы «Mean ж» и «Mean м» содержат средние значения переменных для женщин и мужчин соответственно. То есть, средний возраст женщин составляет 40,68, средний возраст мужчин – 39,15 лет. Средний стаж женщин 17,44, мужчин – 16,87 лет. Далее столбец t-value содержит значение t-критерия, нам оно не надо. Столбец df обозначает количество степеней свободы, нам тоже это не надо. (То есть, приводя в работе результаты статистической обработки данных, неплохо бы эти цифры указать, но расшифровывать не надо). Следующий столбец –p – нужен обязательно. Это то самый уровень достоверности различий средних значений. Наверное, самый важный столбик из этой таблицы.
Теоретическое отступление. Чтобы проверить, различаются ли средние значения в двух группах, сначала мы рассчитываем эти значения. И почти всегда средние значения в двух группах будут хоть сколько-нибудь отличаться. То есть, мы почти всегда получаем НЕ ОДИНАКОВЫЕ средние значения. В нашем примере то же самое – средние значения для женщин и мужчин по всем переменным разные. Но где-то они отличаются больше, где-то – меньше. И «на глаз» мы не можем определить, отличаются ли средние значения «чуть-чуть» или «сильно». Определить это можно только с помощью статистических критериев, например, по t-критерию Стьюдента. Не вдаваясь в подробности расчетов, предлагаю запомнить:
Средние значения в двух группах по какой-либо переменной достоверно отличаются, если показатель p<0,05 (в программе эти переменные выделены красным цветом)
В этом случае говорят также, что различия средних значений являются достоверными (или – статистически значимыми) на 5% уровне.
Иногда, если p больше 0,05, но меньше, чем 0,1, то говорят, что различия есть на уровне статистической тенденции. То есть, это менее выраженные различия.
Но обычно если р>0,05, то говорят, что достоверных различий не выявлено /не установлено /не обнаружено. Но ДАЖЕ ЕСЛИ p>0,1, НЕЛЬЗЯ ГОВОРИТЬ, ЧТО СРЕДНИЕ ЗНАЧЕНИЯ ОДИНАКОВЫЕ.
Таким образом, в данном случае для мужчин и женщин достоверно отличаются только показатели профессионального стресса (значение р=0,029, это меньше, чем 0,05). На уровне тенденции есть различия по показателю Маслач_2 (здесь р=0,051, это больше, чем 0,05, но меньше, чем 0,1). Для других переменных достоверных отличий не выявлено.
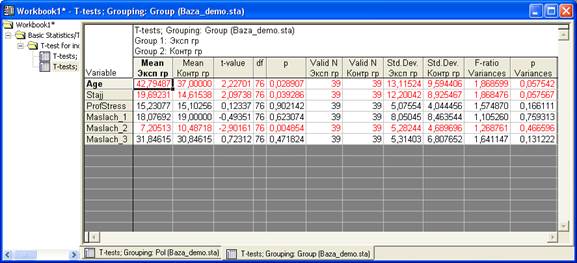
Теперь рассмотрим сравнение средних значений в экспериментальной и контрольной группе. Снова в верхнем меню выберите пункт Statistics – в нём Basic Statistics/Tables. Поскольку мы уже запустили этот модуль программы, то на экране появится окно
Можно выбрать «Continue current», чтобы продолжить расчет. Чтобы перейти к сравнению экспериментальной и контрольной группы, щелкните кнопку Variable. В правой части окна – Grouping variable – выберите переменную номер 2. Нажмите ОК. Нажмите Summary, как на картинках выше. Получим такой результат.
Обратите внимание, что для участников экспериментальной и контрольной группы достоверно отличается средний возраст, средний стаж и средние значения по показателю Маслач_2. По другим переменным достоверных отличий не выявлено.
Как закрыть программу.
Сначала надо закрыть все расчеты. Для этого в нижнем левом углу щелкните на прямоугольник, откроется окно расчетов, закрывайте его крестиком или кнопкой Cancel. Вторым шагом закрывайте окно Workbook1 – тоже крестиком. Этот файл можно сохранить, но это не обязательно. Третий шаг – закрывайте файл с данными. Четвертое – закрывайте программу.
Позже допишу: Сравнение средних значений в двух группах – непараметрический метод. Сравнение средних значений в трех и более группах – дисперсионный анализ
|

 выберите, нажмите ОК.
выберите, нажмите ОК.

 Теперь ОК.
Теперь ОК.