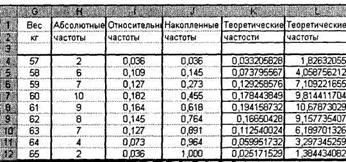
Решение. 1. Определите абсолютные, относительные и накопленные частоты для данной выборки.

1. Определите абсолютные, относительные и накопленные частоты для данной выборки.

2. Найдите теоретические частоты нормального распределения. Для этого пред­варительно необходимо найти среднее значение и стандартное отклонение вы­борки.

В ячейке I13 с помощью функции СРЗНАЧ найдите среднее значение для данных из диапазона А2:Е12 (60,855). В ячейке J13 с помощью функции СТАНДОТКЛОН най­дите стандартное отклонение для этих же данных (2,05). В ячейки К1 и К2 введите название столбца — Теоретические частости. Затем с помощью функции НОРМРАСП найдите теоретические частости. Установите курсор в ячейку К4, вызовите указанную функцию и заполните ее рабочие поля: х — G4; Среднее — $1$13; Стандартное_откл — $J$13; Интегральный — 0. Получим в ячейке К4 0,033. Далее протя­гиванием скопируйте содержимое ячейки К4 в диапазон ячеек К5:К12. Затем в ячей­ки L1 и L2 введите название нового столбца — Теоретические частоты. Установите курсор в ячейку L4 и введите формулу =Н$13*К4. Далее протягиванием скопи­руйте содержимое ячейки L4 в диапазон ячеек L5:L12. Результаты вычислений представлены на рис. 4.6.

Рис. 4.6. Результаты вычисления теоретических частостей и частот из примера П3.1

3. С помощью функции ХИ2ТЕСТ определите соответствие данных нормальному закону распределения. Для этого установите табличный курсор в свободную ячейку L13. На панели инструментов Стандартная нажмите кнопку Вставка функ­ции(f_x)., B появившемся диалоговом окне Мастер функций выберите категорию Статистические и функцию ХИ2ТЕСТ, после чего нажмите кнопку ОК. Появившее­ся диалоговое окно ХИ2ТЕСТ отодвиньте вправо на 1-2 см от данных. Указате­лем мыши в рабочие поля введите фактический Н4:Н12 и ожидаемые L4:L12 ди­апазоны частот (рис. 4.7). Нажмите кнопку ОК. В ячейке L13 появится значение вероятности того, что выборочные данные соответствуют нормальному закону распределения — 0,9842.

Рис. 4.7. Пример заполнения рабочих полей функции ХИ2ТЕСТ

4. Поскольку полученная вероятность соответствия экспериментальных данных р = 0,98 много больше, чем уровень значимости a = 0,05, то можно утверждать, что нулевая гипотеза не может быть отвергнута и, следовательно, данные не противоречат нормальному закону распределения. Более того, поскольку по­лученная вероятность р = 0,98 близка к 1, можно говорить о высокой степени вероятности того, что экспериментальные данные соответствуют нормально­му закону.

Пример реализации рассмотренных задач приведен в «Задании 4.3».