Решение. 1. В диапазон А1:А7 введите исходный ряд чисел.
1. В диапазон А1:А7 введите исходный ряд чисел. 2. Далее вызовите процедуру Описательная статистика. Для этого, указав курсором мыши на пункт меню Сервис, выберите команду Анализ данных. Затем в появившемся списке Инструменты анализа выберите строку Описательная статистика. 3. В появившемся диалоговом окне в рабочем поле Входной интервал: укажите входной диапазон —А1:А7. Переключателем активизируйте Выходной интервал и укажите выходной диапазон — ячейку В1. В разделе Группировка переключатель установите в положение по столбцам. Установите флажок в левое поле Уровень 4. В результате анализа в указанном выходном диапазоне для доверительной вероятности 0,95 получаем значения доверительного интервала (рис. 4.4).
Рис. 4.4. Исходная выборка (А1:А7) и результат вычислений (СЗ) из примера 4.2
Уровень надежности — это половина доверительного интервала для генерального среднего арифметического. Из полученного результата следует, что с вероятностью 0,95 среднее арифметическое для генеральной совокупности находится в интервале 18,571 ± 3,77. Здесь 18,571 — выборочное среднее М для рассматриваемого примера, которое находится обычно процедурой Описательная статистика одновременно с доверительным интервалом. 5. Для нахождения доверительных границ для «выскакивающей» варианты необходимо полученный выше доверительный интервал умножить на Таким образом, варианта, попадающая в интервал 18,571 ± 9,975, считается принадлежащей данной совокупности с вероятностью 0,95. Выходящая за эти границы может быть отброшена с уровнем значимости a = 0,05. Проверка соответствия теоретическому распределению. Следующей задачей, возникающей при анализе одной выборки, является оценка меры соответствия (расхождения) полученных эмпирических данных и каких-либо теоретических распределений. Это связано с тем, что в большинстве случаев при решении реальных задач закон распределения и его параметры неизвестны. В то же время применяемые статистические методы в качестве предпосылок часто требуют определенного закона распределения. Наиболее часто проверяется предположение о нормальном распределении генеральной совокупности, поскольку большинство статистических процедур ориентировано на выборки, полученные из нормально распределенной генеральной совокупности. Для оценки соответствия имеющихся экспериментальных данных нормальному закону распределения обычно используют графический метод, выборочные параметры формы распределения и критерии согласия.
Графический метод позволяет давать ориентировочную оценку расхождения или совпадений распределений (рис. 4.5).
При большом числе наблюдений ( Наиболее убедительные результаты дает использование критериев согласия. Критериями согласия называют статистические критерии, предназначенные для проверки согласия опытных данных и теоретической модели. Здесь нулевая гипотеза Но представляет собой утверждение о том, что распределение генеральной совокупности, из которой получена выборка, не отличается от нормального. Среди критериев согласия большое распространение получил непараметрический критерий Для определения степени соответствия реального распределения нормальному можно воспользоваться критерием
Отметим, что сколько-нибудь уверенно о нормальности закона распределения можно судить, если имеется не менее 50 результатов наблюдений. В случаях меньшего числа данных можно говорить только о том, что данные не противоречат нормальному закону, и в этом случае обычно используют графические методы оценки соответствия. При большем числе наблюдений целесообразно совместное использование графических и статистических (например, тест хи-квадрат или аналогичные) методов оценки, естественно дополняющих друг друга. Использование критерия согласия хи-квадрат. Для применения критерия желательно, чтобы объем выборки Отметим, что сравниваться должны именно абсолютные частоты, а не относительные (частости). При этом, как и любой другой статистический критерий, критерий хи-квадрат не доказывает справедливость нулевой гипотезы (соответствие эмпирического распределения нормальному), а лишь может позволить ее отвергнуть с определенной вероятностью (уровнем значимости). В MS Excel критерий хи-квадрат реализован в функции ХИ2ТЕСТ. Функция ХИ2ТЕСТ вычисляет вероятность совпадения наблюдаемых (фактических) значений и теоретических (гипотетических) значений. Если вычисленная вероятность ниже уровня значимости (0,05), то нулевая гипотеза отвергается и утверждается, что наблюдаемые значения не соответствуют нормальному закону распределения. Если вычисленная вероятность близка к 1, то можно говорить о высокой степени соответствия экспериментальных данных нормальному закону распределения. Функция имеет следующие параметры: ХИ2ТЕСТ (фактический_интервал; ожидае-мый_интервал). Здесь: * фактический_интервал — это интервал данных, которые содержат наблюдения, подлежащие сравнению с ожидаемыми значениями; * ожидаемый интервал — это интервал данных, который содержит теоретические (ожидаемые) значения для соответствующих наблюдаемых. Пример 4.3. Проверить соответствие выборочных данных (64,57, 63, 62, 58, 61, 63, 60, 60, 61, 65, 62, 62, 60, 64, 61, 59, 59, 63, 61, 62, 58, 58, 63, 61, 59, 62, 60, 60, 58, 61, 60, 63, 63, 58, 60, 59, 60, 59, 61, 62, 62, 63, 57, 61, 58, 60, 64, 60, 59, 61, 64, 62, 59, 65) нормальному закону распределения.
|


 (в примере —
(в примере —  , то есть 3,77*
, то есть 3,77*  = 7 и нажмите ОК. В результате получим в ячейке С4 значение доверительного интервала — 9,975.
= 7 и нажмите ОК. В результате получим в ячейке С4 значение доверительного интервала — 9,975.
 > 100) неплохие результаты дает вычисление выборочных параметров формы распределения: эксцесса и асимметрии. Принято говорить, что предположение о нормальности распределения не противоречит имеющимся данным, если асимметрия близка к нулю, то есть лежит в диапазоне от -0,2 до 0,2, а эксцесс — от 2 до 4.
> 100) неплохие результаты дает вычисление выборочных параметров формы распределения: эксцесса и асимметрии. Принято говорить, что предположение о нормальности распределения не противоречит имеющимся данным, если асимметрия близка к нулю, то есть лежит в диапазоне от -0,2 до 0,2, а эксцесс — от 2 до 4. (хи-квадрат). Он основан на сравнении эмпирических частот интервалов группировки с теоретическими (ожидаемыми) частотами, рассчитанными по формулам нормального распределения.
(хи-квадрат). Он основан на сравнении эмпирических частот интервалов группировки с теоретическими (ожидаемыми) частотами, рассчитанными по формулам нормального распределения.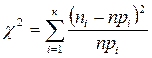 ,
,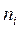 - относительная частота попадания случайной величины в
- относительная частота попадания случайной величины в  -й интервал;
-й интервал; 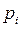 - вероятность попадания случайной величины в i –й интервал в соответствии с нормальным законом распределения
- вероятность попадания случайной величины в i –й интервал в соответствии с нормальным законом распределения > 40, выборочные данные были сгруппированы в интервальный ряд с числом интервалов не менее 7, а в каждом интервале находилось не менее 5 наблюдений (частот).
> 40, выборочные данные были сгруппированы в интервальный ряд с числом интервалов не менее 7, а в каждом интервале находилось не менее 5 наблюдений (частот).


