Лабораторная работа №1
Лабораторная работа №1 ЗНАКОВЫЕ ОРГРАФЫ.
ОПРЕДЕЛЕНИЯ. ОСНОВНЫЕ ПОНЯТИЯ. 1. В ЗО от вершины U к V проводится дуга, если изменение U оказывает непосредственное существенное воздействие на V. Эта дуга имеет знак (+), если воздействие является «усилением» (при прочих равных условиях увеличение U приводит к увеличению V) и знак (-), если воздействие вызывает «торможение» (при прочих равных условиях увеличение U приводит к уменьшению V и уменьшение U приводит к увеличению V). 2. Всякий ЗО можно представить целочисленно-взвешенным орграфом с весами W(U,V)=1, если дуга (U,V) имеет знак (+) и W(U,V)= -1, если дуга (U,V) имеет знак (–). 3. Знак пути (замкнутого пути, контура и т.д.)- есть произведение знаков его дуг, если в произведении знак (+) заменяется на +1, знак (-) на –1. В пути, контуры, полупути могут входить и петли. Для структурного анализа ЗО удобно перейти от ЗО к обычным орграфам и использовать матричный аппарат. Матрица смежности
i, jÎ{1, 2, …n} n- число вершин орграфа Матрица достижимости
СОБСТВЕННЫЙ ВЕКТОР. СОБСТВЕННОЕ ЗНАЧЕНИЕ. Пусть Число l называется собственным значением, соответствующим вектору Например:
значит В линейной алгебре доказано, что l является собственным значением матрицы тогда и только тогда, когда det½M-lI½=0 (1) Определитель det равен сумме произведений по одному из каждой строки и каждого столбца, причем каждое слагаемое входит с соответствующим знаком. В результате получается выражение, являющееся многочленом по l. Многочлен по l называется характеристическим многочленом матрицы M[n] и обозначается как C(l). Доказано, что собственные значения матрицы M[n] в точности совпадают с корнями характеристического многочлена, т.е. являются такими числами l, которые удовлетворяют уравнению: C (l)=0 (2) Уравнение (2) называется характеристическим уравнением матрицы M[n]. Если некоторое собственное значение оказывается кратным корнем для C(l), то количество одинаковых собственных значений совпадают с его кратностью. Если M[n] – диагональная матрица, то собственные значения такой матрицы совпадают с ее диагональными элементами. Если M[n] – одноэлементная матрица, т.е. M = t, тогда C(l)=t- l и поэтому является единственным собственным значением. Если матрицу M[n] рассматривать как матрицу смежности A[n], то матрице будет соответствовать некоторый ВО или ЗО. Тогда собственные значения матрицы A[n] будут собственными значениями ВО или ЗО. Отметим, что собственные значения ВО или ЗО могут использоваться для оценивания устойчивости моделей, задаваемых такими орграфами, при воздействии на такие модели в дискретные моменты времени t=0,1,2,… неких возмущающих факторов. Пример.
Рассмотрим ВО D = (V, A) на рис.1 Рис.1 D = (V, A) Матрица смежности ВО:
Из уравнения C(l) = 0 следует, что собственные значения ВО равны 1, 4, -4. Далее найдем собственный вектор, соответствующий, например, собственному значению l = 4. Предположим, что U[3](1) = <r1, r1, r1> и такой вектор существует. Тогда
Т.е. получим 3 уравнения:
Решениями этих уравнений будут все векторы, записываемые в виде Т.к. собственный вектор по определению ненулевой, то x должен быть отличен от нуля. Таким образом, собственные вектора, соответствующие l=4, представимы в виде всевозможных произведений вектора Аналогично можно показать, что собственные векторы, соответствующие собственным значениям –4 и 1, получаются путем умножения на произвольные ненулевые числа соответственно векторов
Существует теорема о собственных значениях ВО, позволяющая свести к аналогичной задаче для меньших подграфов (теорема не приводится). Отметим, что характеристический многочлен матрицы смежности ВО равен произведению характеристических многочленов матриц смежности его сильных компонент. Пример.
Рис. D = (V, A)
Сильные компоненты:
Собственные значения сильных компонент: K1:
K2: l={8} K3: Матрица смежности A[5] имеет собственные значения Характеристический многочлен ВО на рис.2:
|





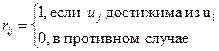
 - квадратная матрица действительных чисел. Ненулевой n-мерный вектор вектор-строка
- квадратная матрица действительных чисел. Ненулевой n-мерный вектор вектор-строка  называется собственным (характеристическим) вектором, если для некоторого скалярного l выполняется соотношение
называется собственным (характеристическим) вектором, если для некоторого скалярного l выполняется соотношение  .
.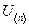 и может принимать как действительное, так и комплексное значение.
и может принимать как действительное, так и комплексное значение.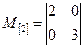

 ,
, - собственный вектор для M с собственным значением l.
- собственный вектор для M с собственным значением l.



 , т.е.
, т.е.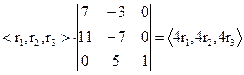


 .
. на числа, отличные от нуля.
на числа, отличные от нуля. и
и 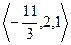 .
.




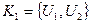

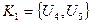


 ,
, ,
, 
 ; 8;
; 8;  .
.



