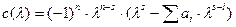МЕТОДЫ ОЦЕНКИ УСТОЙЧИВОСТИ.
Понятие абсолютной устойчивости требует, чтобы значение Vj(t) вершины Uj не было бы слишком большим по абсолютной величине. Понятие импульсной устойчивости требует, чтобы изменение значения Vj(t) вершины Uj, т.е.импульс Pj(t) не был бы слишком большим по абсолютной величине. Вершина Uj называется импульсно устойчивой в импульсном процессе, если последовательность Вершина Uj абсолютно устойчива, если последовательность ВО называется импульсно (абсолютно) устойчивым в импульсном процессе, если этим свойством обладает каждая его вершина. В любом импульсном процессе абсолютная устойчивость (в вершине Uj) означает и импульсную устойчивость (в вершине Uj). С другой стороны, импульсная устойчивость не влечет абсолютной устойчивости. Например,
В простом импульсном процессе с начальной вершиной U1 импульс Pj(t) всегда равен 0 или 1, т.е. ВО – импульсно устойчив, но U1(t) увеличивается на 1 через каждые 2 периода. Это и означает импульсную устойчивость, но не абсолютную устойчивость. Импульсная или абсолютная устойчивость для ВО(ЗО) предупреждает, что системе что-то должно случиться. Это вынуждает изменить ее фундаментальную структуру прежде, чем какие-либо значения вершин или импульсы станут слишком велики. Устойчивость графа связана с его собственными значениями.
ТЕОРЕМА 4. Если ВО D импульсно устойчив для всех простых импульсных процессов, то каждое собственное значение D по абсолютной величине не превосходит единицу. ИЛИ: Если ВО имеет собственное значение, превосходящее по абсолютной величине единицу, то D импульсно неустойчив для некоторого простого импульсного процесса. СЛЕДСТВИЕ ТЕОРЕМЫ 4: Если целочисленно-взвешенный орграф D импульсно устойчив для любых импульсных процессов, то каждое ненулевое собственное значение по абсолютной величине равно 1. Теорему 4 можно применять и к ЗО.
Таким образом, λ = 2 и есть ненулевое собственное значение. По теореме 4 этот ВО импульсно неустойчив для некоторого простого импульсного процесса. Другими словами, найдется такая вершина, в которую поступает начальный импульс, что в некой вершине импульс станет сколь угодно большим. Однако этот ВО не является импульсно неустойчивым для всех простых импульсных процессов (например, с начальной вершиной U5). Теорема, обратная к теореме 4, справедлива только, если ненулевые собственные значения ВО или ЗО различны, т.е. нет кратных собственных значений за исключением, возможно, нулевых. ТЕОРЕМА 5. Пусть все ненулевые собственные значения ВО D = (V,A) различны и не превосходят по абсолютной величине 1. Тогда D импульсно устойчив для всех простых импульсных процессов. (Если ненулевые собственные значения являются кратными, то теорема 5 не применяется). ТЕОРЕМА 6. ВО D абсолютно устойчив для любого простого импульсного процесса тогда и только тогда, когда D импульсно устойчив для любого простого импульсногопроцесса и среди собственных значений нет равного единице. Орграф называется розой, если он состоит из центральной вершины x и непересекающихся контуров, выходящих из x. Обобщенная роза- это сильно связный орграф D,центральная вершина которого принадлежит всем его контурам. Всякая роза оказывается и обобщенной розой. Пусть орграф D-обобщенная роза. ai – сумма знаков контуров длины i, если (+) считается как +1, а (-) как (-1) s – такое наибольшее число, что Если ai = 0 при всех i, то s = 0 Если s = 0, орграф D импульсно и абсолютно устойчив для всех простых импульсных процессов. Если s > 0, то свойства устойчивости орграфа D полностью определяются так называемой лепестковой последовательностью <a1, a2, …, as>. ТЕОРЕМА 7. Если две обобщенные розы D1 и D2 имеют одинаковые лепестковые последовательности, то орграфы D1 и D2 импульсно (абсолютно) устойчивы для всех простых импульсных процессов одновременно. ТЕОРЕМА 8. Пусть D – обобщенная знаковая роза с лепестковой последовательностью <a1, a2, …, as>, s>0. Если D импульсно устойчив для всех простых импульсных процессов, то а) б) ТЕОРЕМА 9. Пусть орграф D – обобщенная знаковая роза с лепестковой последовательностью <a1, a2, …, as>, s>0 и D – импульсно устойчив для всех простых импульсных процессов. Тогда D абсолютно устойчив для всех простых импульсных процессов тогда и только тогда, когда Однако, делать вывод об импульсной устойчивости, основываясь на теореме 8 нельзя, т.к. она дает необходимое, но не достаточное условие. Свойство импульсной устойчивости необходимо проверить, используя другие методы (например, теорема 5). Характеристический многочлен обобщенной розы в общем виде:
Задание на работу:
Дана матрица смежности соответствующего знакового орграфа. Исследовать орграф (согласно порядковому номеру в группе) на устойчивость (импульсную и абсолютную).
Вариант 1
Вариант 2
Вариант 3
Вариант 4
Вариант 5
Вариант 6
Вариант 7
Вариант 8
Вариант 9
Вариант 10
Вариант 11
Вариант 12
Вариант 13
Вариант 14
Вариант 15
Вариант 16
Вариант 17
Вариант 18
Вариант 19
Вариант 20
Вариант 21
Вариант 22
Вариант 23
Вариант 24
|
ограничена, т.е. найдется такое положительное число B, что 
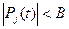для всех t.
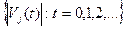ограничена.
Пример.
.
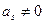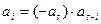i = 1, 2, …, s-1
.
