ИМПУЛЬС. АВТОНОМНЫЙ ИМПУЛЬСНЫЙ ПРОЦЕСС.
Для более глубокого анализа модели в виде ВО необходимо примять некоторые допущения о влиянии изменений значения параметра одной величины на параметры других величин. Такие допущения называются правилами изменения значений параметров вершин. Чтобы определить правило изменения значений параметров вершин, рассмотрим ЗО. Каждая вершина Ui (i=1,2,…,n) принимает значение Vi(t) в дискретные моменты времени t = 0,1,2,… Значение Vi(t+1) определяется значением Vi(t) и информацией о том, увеличили или уменьшили свои значения другие вершины Uj, смежные с Ui, в момент t. Если дуга (Uj,Ui) положительна (отрицательна), то изменение в Uj в момент времени t учитывается со знаком + (-) в Ui в момент t+1. Будем считать, что единичное изменение в Uj влечет единичное изменение в Ui. Изменение Для Автономный импульсный процесс в ЗО определяется по правилу (3) с вектором начальных значений
Часто автономный импульсный процесс определяется вектором исходных значений:
Условие (3) для ВО:
где W(Uj, Ui) = 0, если дуга отсутствует или Простым импульсным процессом с начальной вершиной Ui называется автономный импульсный процесс, в котором вектор P<n>(0) имеет i-ую компоненту равную 1, а остальные компоненты равны 0. В таком процессе начальный единичный импульс в вершине Ui распространяется за некоторое время по всей системе. ТЕОРЕМА 1. Для простого импульсного процесса в ЗО D = (V,A) с начальной вершиной Ui величины Pj(t) и Vj(t) при t>0 определяются:
где ТЕОРЕМА 2. Пусть D-ВО с матрицей смежности A[n] . Для простого импульсного процесса в D с начальной вершиной Ui имеем: Pj(t) = {элемент ij матрицы At[n]} Vj(t) = Vj(исх) + {элемент ij в матрице I[n] + A[n] + A2[n] + …+ At[n]} Vj(t) = Vj(0) + {элемент ij в матрице A[n] + A2[n] + …+ At[n]} ТЕОРЕМА 3. В векторном обозначении для автономного импульсного процесса в ВО с начальной вершиной Ui имеем: P<n>(t) = P<n>(0)*At[n] Где P<n>(0) = <0,0,…,1,0,…,0> с 1 на i-ом месте. Уравнение (5) в векторном виде: P<n>(t+1) = P<n>(t)*A[n]
|

 называется импульсом (при t > 0).
называется импульсом (при t > 0). (3)
(3) и вектором, задающим внешний импульс, вводимый в каждую вершину Uj в момент t = 0:
и вектором, задающим внешний импульс, вводимый в каждую вершину Uj в момент t = 0: .
.
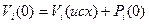 .
. (4)
(4)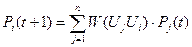 (5)
(5)

 -«знаковый индекс путей» из Ui вUj длины не более t.
-«знаковый индекс путей» из Ui вUj длины не более t.


