Стереографическая проекция
Важное свойство любой карты - сохранение углов (угол между любыми двумя линиями на карте должен быть таким же, как угол между прообразами этих линий на земной поверхности). Сохранение углов особенно важно для мореплавания и аэронавтики, так как оно означает, что наблюдаемый угол между любыми двумя ориентирами равен углу, измеряемому на карте с помощью транспортира. Кроме того, на такой карте остаются неизменными и площади малых областей. Карты, сохраняющие углы, называются конформными. Проще всего построить конформную карту с помощью стереографической проекции. На рис. 8.8 показано, как поверхность сферы в точке
Рис. 8.8. Три проекции Обозначим за долготу и дополнение до широты точки на сфере буквами
Здесь и в дальнейшем радиус считается равным единице. Ось
|

 проецируется из точки
проецируется из точки  (принадлежащей сфере) на плоскость, касательную к сфере в диаметрально противоположной точке (антипод точки
(принадлежащей сфере) на плоскость, касательную к сфере в диаметрально противоположной точке (антипод точки 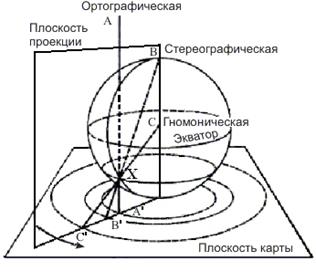
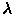 и
и 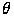 соответственно,
соответственно,  , а через
, а через 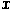 и
и  - координаты проекций этой точки в некоторой декартовой системе координат, заданной на плоскости проекции. Соответствующие формулы проецирования для Северного полушария имеют следующий вид:
- координаты проекций этой точки в некоторой декартовой системе координат, заданной на плоскости проекции. Соответствующие формулы проецирования для Северного полушария имеют следующий вид: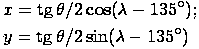
 направлена вдоль меридиана 135°.
направлена вдоль меридиана 135°.


