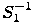Ортогональные проекции
Сначала рассмотрим математическое описание параллельных проекций как более простых. Случай, когда картинная плоскость перпендикулярна оси Случай аксонометрической проекции сводится к последовательности преобразований, подобно тому, как осуществлялся поворот в пространстве относительно произвольной оси. Пусть плоскость задается единичным вектором нормали
Вектор, направленный по нормали от начала координат до пересечения с плоскостью, есть
Координаты вектора единичной нормали являются ее направляющими косинусами. Проецирование в пространстве однородных координат осуществляется следующей последовательностью шагов. Сдвиг на вектор
Поворот, совмещающий направление нормали с направлением оси Проекция на плоскость
Поворот с помощью матрицы Сдвиг на вектор Полное преобразование, таким образом, определяется матрицей
|
и задается уравнением 
(т.е. ортографическая проекция), фактически уже рассматривался в лекции 5, где был приведен вид матриц проекции на координатные плоскости.
и расстоянием от начала координат 
. Каноническое уравнение плоскости, таким образом, имеет вид
с помощью матрицы
, а затем - поворот относительно оси 
до совмещения нормали с осью 
.
с помощью матрицы
.
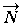с помощью матрицы 
