Теперь разберем один способ использования метода художника при изображении пространственных сцен, содержащих несколько объектов или составные объекты. Это так называемый метод двоичного разбиения пространства плоскостями. Плоскости, как обычно, будут задаваться с помощью вектора нормали 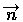 и расстояния до начала координат
и расстояния до начала координат 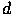 (с точностью до знака). Пусть изображаемая сцена состоит из набора непересекающихся граней
(с точностью до знака). Пусть изображаемая сцена состоит из набора непересекающихся граней 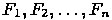 (они могут иметь общие прямолинейные участки границы). Проведем плоскость
(они могут иметь общие прямолинейные участки границы). Проведем плоскость 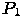 , разбивающую все пространство на два полупространства, в одном из которых находится наблюдатель. Предположим, что плоскость при этом не пересекает ни одну из граней (но может содержать участок ее границы). Тогда грани, находящиеся в одном полупространстве с наблюдателем, могут заслонять от него часть граней из второго полупространства, но не наоборот. Это означает, что они должны изображаться позже. Разобьем плоскостью
, разбивающую все пространство на два полупространства, в одном из которых находится наблюдатель. Предположим, что плоскость при этом не пересекает ни одну из граней (но может содержать участок ее границы). Тогда грани, находящиеся в одном полупространстве с наблюдателем, могут заслонять от него часть граней из второго полупространства, но не наоборот. Это означает, что они должны изображаться позже. Разобьем плоскостью 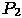 второе полупространство и снова определим, какая группа граней из него должна изображаться раньше. Продолжая этот процесс до того уровня, когда все пространство будет разбито плоскостями на секции, в каждой из которых будет находиться только одна грань, мы получим упорядоченный набор граней. Этот порядок можно изобразить в виде двоичного дерева. В контексте рассматриваемого алгоритма это дерево представляет собой структуру данных
второе полупространство и снова определим, какая группа граней из него должна изображаться раньше. Продолжая этот процесс до того уровня, когда все пространство будет разбито плоскостями на секции, в каждой из которых будет находиться только одна грань, мы получим упорядоченный набор граней. Этот порядок можно изобразить в виде двоичного дерева. В контексте рассматриваемого алгоритма это дерево представляет собой структуру данных 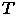 , элементами которой являются указатель на грань изображаемой сцены, плоскость, отделяющая эту грань, указатели на левое и правое поддерево
, элементами которой являются указатель на грань изображаемой сцены, плоскость, отделяющая эту грань, указатели на левое и правое поддерево 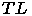 и
и 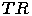 . Такой элемент называется узлом дерева.
. Такой элемент называется узлом дерева.
В каждом узле дерева левое поддерево будет содержать грани, отделенные плоскостью, а правое - не отделенные. Рисование сцены осуществляется с помощью рекурсивного алгоритма следующего вида:

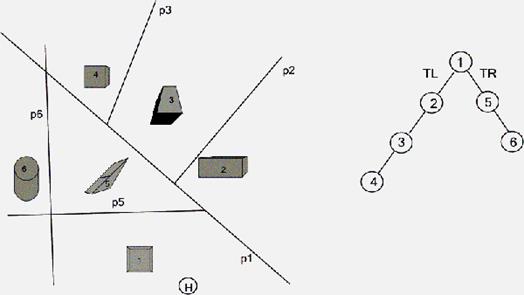
Рис. 7.6. Разбиение пространства и соответствующее ему дерево
Построение плоскостей и дерева в данном случае осуществляется "вручную". Для эффективности работы алгоритма надо стремиться к тому, чтобы дерево было сбалансированным. Если какие-то грани не удается отделить, то их пересекают плоскостями и рисуют как два объекта. Способ определения, по какую сторону плоскости находится наблюдатель, а по какую - грань, очень прост. Параметр плоскости 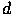 для каждой грани будем задавать так, чтобы грань находилась в положительной полуплоскости. Тогда если при подстановке координат наблюдателя в это уравнение получаем положительное значение, то он находится в одной полуплоскости с гранью, если нет, то в разных.
для каждой грани будем задавать так, чтобы грань находилась в положительной полуплоскости. Тогда если при подстановке координат наблюдателя в это уравнение получаем положительное значение, то он находится в одной полуплоскости с гранью, если нет, то в разных.
Алгоритм может применяться не только к многогранникам, но и вообще к любой сцене при условии, что имеется алгоритм изображения составляющих ее объектов. На рис. 7.6 изображена проекция сцены, разбитой вертикальными плоскостями, и соответствующее ей дерево. Положение наблюдателя отмечено кружком с буквой Н. При этой точке зрения объекты будут изображаться в последовательности 5, 6, 1, 2, 3, 4.

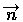 и расстояния до начала координат
и расстояния до начала координат 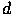 (с точностью до знака). Пусть изображаемая сцена состоит из набора непересекающихся граней
(с точностью до знака). Пусть изображаемая сцена состоит из набора непересекающихся граней 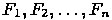 (они могут иметь общие прямолинейные участки границы). Проведем плоскость
(они могут иметь общие прямолинейные участки границы). Проведем плоскость 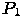 , разбивающую все пространство на два полупространства, в одном из которых находится наблюдатель. Предположим, что плоскость при этом не пересекает ни одну из граней (но может содержать участок ее границы). Тогда грани, находящиеся в одном полупространстве с наблюдателем, могут заслонять от него часть граней из второго полупространства, но не наоборот. Это означает, что они должны изображаться позже. Разобьем плоскостью
, разбивающую все пространство на два полупространства, в одном из которых находится наблюдатель. Предположим, что плоскость при этом не пересекает ни одну из граней (но может содержать участок ее границы). Тогда грани, находящиеся в одном полупространстве с наблюдателем, могут заслонять от него часть граней из второго полупространства, но не наоборот. Это означает, что они должны изображаться позже. Разобьем плоскостью 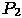 второе полупространство и снова определим, какая группа граней из него должна изображаться раньше. Продолжая этот процесс до того уровня, когда все пространство будет разбито плоскостями на секции, в каждой из которых будет находиться только одна грань, мы получим упорядоченный набор граней. Этот порядок можно изобразить в виде двоичного дерева. В контексте рассматриваемого алгоритма это дерево представляет собой структуру данных
второе полупространство и снова определим, какая группа граней из него должна изображаться раньше. Продолжая этот процесс до того уровня, когда все пространство будет разбито плоскостями на секции, в каждой из которых будет находиться только одна грань, мы получим упорядоченный набор граней. Этот порядок можно изобразить в виде двоичного дерева. В контексте рассматриваемого алгоритма это дерево представляет собой структуру данных 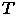 , элементами которой являются указатель на грань изображаемой сцены, плоскость, отделяющая эту грань, указатели на левое и правое поддерево
, элементами которой являются указатель на грань изображаемой сцены, плоскость, отделяющая эту грань, указатели на левое и правое поддерево 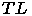 и
и 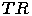 . Такой элемент называется узлом дерева.
. Такой элемент называется узлом дерева.




