Алгоритм Робертса
Этот алгоритм, предложенный в 1963 г., является первой разработкой такого рода и предназначен для удаления невидимых линий при штриховом изображении объектов, составленных из выпуклых многогранников. Он относится к алгоритмам, работающим в объектном пространстве, и очень элегантен с математической точки зрения. В нем очень удачно сочетаются геометрические методы и методы линейного программирования. Выпуклый многогранник однозначно определяется набором плоскостей, образующих его грани, поэтому исходными данными для алгоритма являются многогранники, заданные списком своих граней. Грани задаются в виде плоскостей, заданных в канонической форме (см. лекцию 3) в объектной системе координат:
Рис. 7.2. Внешние нормали тетраэдра Таким образом, каждая плоскость определяется четырехмерным вектором
Принадлежность точки плоскости можно установить с помощью скалярного произведения, т.е. если
Умножая столбцы матрицы на вектор В своем алгоритме Робертс рассматривает только отрезки, являющиеся пересечением граней многогранника. Из обобщенной матрицы можно получить информацию о том, какие грани многогранника пересекаются в вершинах. Действительно, если вершина
Эту систему можно записать в матричном виде:
где
т.е. они составляют последнюю строку обратной матрицы. А это означает, что если для каких-либо трех плоскостей обратная матрица существует, то плоскости имеют общую вершину. Алгоритм прежде всего удаляет из каждого многогранника те ребра или грани, которые экранируются самим телом. Робертс использовал для этого простой тест: если одна или обе смежные грани обращены своей внешней поверхностью к наблюдателю, то ребро является видимым. Тест этот выполняется вычислением скалярного произведения координат наблюдателя на вектор внешней нормали грани: если результат отрицательный, то грань видима. Затем каждое из видимых ребер каждого многогранника сравнивается с каждым из оставшихся многогранников для определения того, какая его часть или части, если таковые есть, экранируются этими телами. Для этого в каждую точку ребра проводится отрезок луча, выходящего из точки расположения наблюдателя. Если отрезок не пересекает ни одного из многогранников, то точка видима. Для решения этой задачи используются параметрические уравнения прямой, содержащей ребро, и луча. Если заданы концы отрезка
а прямая, идущая в точку, соответствующую параметру
Для определения той части отрезка, которая закрывается каким-либо телом, достаточно найти значения
Эти условия должны выполняться для всех плоскостей. Полагая Так как объем вычислений растет с увеличением числа многоугольников, то желательно по мере возможности сокращать их число, т.е. если мы аппроксимируем некоторую поверхность многогранником, то в качестве граней можно использовать не треугольники, а более сложные многоугольники. При этом, встает проблема, как построить такой многоугольник, чтобы он мало отклонялся от плоской фигуры.
|

 .
.
 , а каждая точка
, а каждая точка  , заданная в однородных координатах, также представляет собой четырехмерный вектор:
, заданная в однородных координатах, также представляет собой четырехмерный вектор:
 , то точка принадлежит плоскости, если же нет, то знак произведения показывает, по какую сторону от плоскости эта точка находится. В алгоритме Робертса плоскости строятся таким образом, что внутренние точки многогранника лежат в положительной полуплоскости. Это означает, что вектор
, то точка принадлежит плоскости, если же нет, то знак произведения показывает, по какую сторону от плоскости эта точка находится. В алгоритме Робертса плоскости строятся таким образом, что внутренние точки многогранника лежат в положительной полуплоскости. Это означает, что вектор  является внешней нормалью к многограннику (рис. 7.2). Из векторов плоскостей строится прямоугольная матрица порядка
является внешней нормалью к многограннику (рис. 7.2). Из векторов плоскостей строится прямоугольная матрица порядка  , которая называется обобщенной матрицей описания многогранника:
, которая называется обобщенной матрицей описания многогранника:
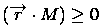 (имеется в виду умножение вектор-строки на матрицу).
(имеется в виду умножение вектор-строки на матрицу). принадлежит граням
принадлежит граням  , то она удовлетворяет уравнениям
, то она удовлетворяет уравнениям

 - матрица, составленная из вектор-столбцов
- матрица, составленная из вектор-столбцов  . Значит, координаты вершины определяются соотношением
. Значит, координаты вершины определяются соотношением
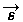 , а наблюдатель расположен в точке
, а наблюдатель расположен в точке  , то отрезок задается уравнением
, то отрезок задается уравнением
 , - уравнением
, - уравнением
 , при которых произведение вектора
, при которых произведение вектора  на обобщенную матрицу положительно. Для каждой плоскости
на обобщенную матрицу положительно. Для каждой плоскости  записывается неравенство
записывается неравенство
 , получаем систему уравнений, решения которой дают нам точки "смены видимости" отрезка. Результат можно получить путем совместного решения всевозможных пар уравнений из этой системы. Число всевозможных решений при
, получаем систему уравнений, решения которой дают нам точки "смены видимости" отрезка. Результат можно получить путем совместного решения всевозможных пар уравнений из этой системы. Число всевозможных решений при  плоскостях равно
плоскостях равно  .
.


