От задачи отсечения отрезков можно перейти к более сложной: клиппирование произвольных многоугольников. Если многоугольник невыпуклый, то в результате пересечения даже с прямоугольным окном может получиться несколько не связанных между собой фигур, как это показано на рис. 6.8.

Рис. 6.8. Отсечение невыпуклого многоугольника
Когда стоит задача штрихования замкнутой области одновременно с задачей отсечения, то важно правильно определить принадлежность вновь полученных фигур внутренней или внешней части исходного многоугольника. Пусть исходный многоугольник задан упорядоченным списком вершин  , соответствующих ребрам
, соответствующих ребрам  . Для отсечения такого многоугольника прямоугольным окном можно применить алгоритм, предложенный Сазерлендом и Ходжменом. Идея его заключается в последовательном отсечении части многоугольника прямыми, соответствующими сторонам окна. Результатом его работы является упорядоченный список вершин, лежащих в видимой части окна. На каждом шаге алгоритма образуется некоторая промежуточная фигура, также представленная упорядоченным списком вершин и ребер. Пример таких последовательных отсечений показан на рис. 6.9. В процессе отсечения последовательно обходится список вершин, причем каждая очередная точка за исключением первой рассматривается как конечная точка ребра, начальной точкой которого является предшествующая точка из списка. Порядок, в котором рассматриваются стороны окна, не имеет значения. В процессе обхода формируется список новых вершин многоугольника.
. Для отсечения такого многоугольника прямоугольным окном можно применить алгоритм, предложенный Сазерлендом и Ходжменом. Идея его заключается в последовательном отсечении части многоугольника прямыми, соответствующими сторонам окна. Результатом его работы является упорядоченный список вершин, лежащих в видимой части окна. На каждом шаге алгоритма образуется некоторая промежуточная фигура, также представленная упорядоченным списком вершин и ребер. Пример таких последовательных отсечений показан на рис. 6.9. В процессе отсечения последовательно обходится список вершин, причем каждая очередная точка за исключением первой рассматривается как конечная точка ребра, начальной точкой которого является предшествующая точка из списка. Порядок, в котором рассматриваются стороны окна, не имеет значения. В процессе обхода формируется список новых вершин многоугольника.

Рис. 6.9. Последовательные шаги клиппирования произвольного многоугольника
На первом шаге для первой вершины в списке определяется ее принадлежность видимой области. Если она видима, то она становится первой точкой первого обрабатываемого ребра и заносится в список новых вершин. Если же она невидима, то в список новых вершин не заносится, но все равно становится первой точкой ребра.
Для анализируемого ребра возможны четыре случая расположения относительно окна.
- Ребро полностью видимо. Очередная точка заносится в список новых вершин (предыдущая уже должна находиться в этом списке, поскольку ребро полностью видимо).
- Ребро полностью невидимо. Никаких действий не производится.
- Ребро выходит из области. Находится точка пересечения ребра со стороной окна и заносится в список новых ребер.
- Ребро входит в область. Также отыскивается точка пересечения со стороной окна и заносится в список новых вершин. Конечная точка тоже заносится в список новых вершин.
В этом алгоритме постоянно приходится определять видимость точки по отношению к конкретному ребру отсекающего окна. Окно также можно задать в виде упорядоченного списка вершин. Если обход вершин окна осуществляется по часовой стрелке, то его внутренняя область будет расположена по правую сторону от границы. При этом расположение точки  относительно прямой, которой принадлежит ребро, можно устанавливать различными способами:
относительно прямой, которой принадлежит ребро, можно устанавливать различными способами:
- Выбирается начальная точка
 данного ребра и строится вектор
данного ребра и строится вектор 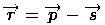 и вектор внутренней нормали
и вектор внутренней нормали  к границе (ребру) окна. Вычисляется скалярное произведение
к границе (ребру) окна. Вычисляется скалярное произведение  . Если
. Если  , то точка
, то точка  является видимой.
является видимой. - Строится пространственный вектор
 (третью координату можно положить равной нулю). Вектор
(третью координату можно положить равной нулю). Вектор  (также пространственный, лежащий в той же плоскости, что и
(также пространственный, лежащий в той же плоскости, что и  ) направлен вдоль ребра (с учетом направления обхода). Вычисляется векторное произведение
) направлен вдоль ребра (с учетом направления обхода). Вычисляется векторное произведение  . Если координата
. Если координата 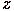 у вектора
у вектора 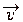 положительна, то точка
положительна, то точка  лежит справа от ребра (является видимой).
лежит справа от ребра (является видимой). - Выписывается каноническое уравнение прямой, проходящей через ребро:

- Для произвольной внутренней точки окна
 вычисляется значение
вычисляется значение  , а также для точки
, а также для точки  вычисляется
вычисляется  . Если числа
. Если числа  и
и  имеют одинаковый знак, то точка
имеют одинаковый знак, то точка  является видимой.
является видимой.
Наиболее просто эти алгоритмы реализуются в случае отсечения прямоугольным окном со сторонами, параллельными осям координат.
Вопросы и упражнения
- Что такое клиппирование?
- Если концы отрезков имеют коды 1000 и 0100, сколько сторон окна он может пересекать?
- При каком значении кода одного из концов отрезка он обязательно будет частично видимым?
- Если оба конца отрезка лежат вне окна, то при каких кодах концов он может проходить вдоль диагонали окна?
- Какой из алгоритмов отсечения отрезков эффективнее: приведенный в блок-схеме 5.3 или основанный на делении отрезка пополам?
- С помощью какого условия можно определить принадлежность точки выпуклому многоугольнику?
- Будет ли это условие применимо в случае произвольного многоугольника? (подтвердите свой ответ примерами).
- Какие случаи расположения ребра относительно окна рассматриваются в алгоритме клиппирования произвольного многоугольника?


 , соответствующих ребрам
, соответствующих ребрам  . Для отсечения такого многоугольника прямоугольным окном можно применить алгоритм, предложенный Сазерлендом и Ходжменом. Идея его заключается в последовательном отсечении части многоугольника прямыми, соответствующими сторонам окна. Результатом его работы является упорядоченный список вершин, лежащих в видимой части окна. На каждом шаге алгоритма образуется некоторая промежуточная фигура, также представленная упорядоченным списком вершин и ребер. Пример таких последовательных отсечений показан на рис. 6.9. В процессе отсечения последовательно обходится список вершин, причем каждая очередная точка за исключением первой рассматривается как конечная точка ребра, начальной точкой которого является предшествующая точка из списка. Порядок, в котором рассматриваются стороны окна, не имеет значения. В процессе обхода формируется список новых вершин многоугольника.
. Для отсечения такого многоугольника прямоугольным окном можно применить алгоритм, предложенный Сазерлендом и Ходжменом. Идея его заключается в последовательном отсечении части многоугольника прямыми, соответствующими сторонам окна. Результатом его работы является упорядоченный список вершин, лежащих в видимой части окна. На каждом шаге алгоритма образуется некоторая промежуточная фигура, также представленная упорядоченным списком вершин и ребер. Пример таких последовательных отсечений показан на рис. 6.9. В процессе отсечения последовательно обходится список вершин, причем каждая очередная точка за исключением первой рассматривается как конечная точка ребра, начальной точкой которого является предшествующая точка из списка. Порядок, в котором рассматриваются стороны окна, не имеет значения. В процессе обхода формируется список новых вершин многоугольника.
 относительно прямой, которой принадлежит ребро, можно устанавливать различными способами:
относительно прямой, которой принадлежит ребро, можно устанавливать различными способами: данного ребра и строится вектор
данного ребра и строится вектор 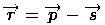 и вектор внутренней нормали
и вектор внутренней нормали  к границе (ребру) окна. Вычисляется скалярное произведение
к границе (ребру) окна. Вычисляется скалярное произведение  . Если
. Если  , то точка
, то точка  является видимой.
является видимой. (третью координату можно положить равной нулю). Вектор
(третью координату можно положить равной нулю). Вектор  (также пространственный, лежащий в той же плоскости, что и
(также пространственный, лежащий в той же плоскости, что и  ) направлен вдоль ребра (с учетом направления обхода). Вычисляется векторное произведение
) направлен вдоль ребра (с учетом направления обхода). Вычисляется векторное произведение  . Если координата
. Если координата 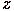 у вектора
у вектора 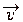 положительна, то точка
положительна, то точка  лежит справа от ребра (является видимой).
лежит справа от ребра (является видимой).
 вычисляется значение
вычисляется значение  , а также для точки
, а также для точки  вычисляется
вычисляется  . Если числа
. Если числа  и
и  имеют одинаковый знак, то точка
имеют одинаковый знак, то точка 


