Алгоритм Сазерленда-Коэна отсечения прямоугольной областью
Рассмотрим плоскую сцену, состоящую из отрезков различной длины и направлений, в которой надо выделить часть, находящуюся внутри прямоугольника. Прямоугольник задан списком ребер: t<op>, b<ottom>, l<eft>, r<ight>;, отрезки также задаются координатами концевых точек. Область, отсекаемая окном (с учетом его границы), состоит из точек
Пусть концы отрезка заданы точками
Рис. 6.1. Коды Сазерленда-Коэна для областей Отрезок полностью невидим, если оба его конца лежат 1. справа от ребра 2. слева от ребра 3. снизу от ребра 4. сверху от ребра Во всех остальных случаях отрезок может (но не обязан) пересекать прямоугольное окно. Для выполнения анализа полной видимости или невидимости отрезка А.Сазерленд и Д.Коэн предложили следующий алгоритм. Прямые, которым принадлежат ребра прямоугольника, разбивают плоскость на девять областей, каждой из которых присваивается четырехразрядный код. Каждый бит этого кода "отвечает" за одну из прямых: 1-й (старший) бит - за прямую Концевым точкам отрезков сцены теперь можно присвоить коды в зависимости от расположения точек. Ясно, что если коды обоих концов отрезка равны нулю, то отрезок полностью лежит внутри окна. Для дальнейшего анализа воспользуемся операцией логического умножения кодов (поразрядное логическое "И"). Тогда таблица истинности для кодов, согласно схеме на рис. 6.1, будет выглядеть следующим образом: Таблица 6.1. Значения истинности для логического умножения кодов областей
Из сопоставления таблицы с рисунком видно, что если произведение кодов концов отрезка принимает значение T<rue>;, то отрезок целиком лежит по одну сторону какой-то из прямых, причем внешнюю сторону по отношению к окну, следовательно, он полностью невидим. Во всех остальных случаях отрезок может частично лежать внутри окна, поэтому для определения их видимой части надо решать задачу о пересечении отрезков с ребрами окна. При этом желательно по возможности сократить число перебираемых пар "отрезок-ребро". В самом общем случае существует две точки пересечения отрезка с ребрами, и эти две точки принимаются за новые концевые точки изображаемого отрезка. Но сначала можно выделить некоторые более простые частные случаи, поиск пересечений для которых является более эффективным. Прежде всего это горизонтальные и вертикальные отрезки, для которых поиск точки пересечения тривиален. Далее, если код одного из концов отрезка равен нулю, то существует только одно пересечение этого отрезка с ребром (или с двумя ребрами, если отрезок проходит через угловую точку окна). На рис. 6.2 приведена общая блок-схема алгоритма отсечения для одного произвольно направленного отрезка. В блок-схеме используются следующие соглашения и обозначения: · входными данными являются точки · на выходе получаем новые концевые точки · используются следующие вспомогательные функции: GetCode(r) - определение кода точки; Intersec0(r1,l) - поиск пересечения отрезка со сторонами окна при условии, что обе точки лежат вне окна; если пересечения нет, устанавливает переменную IsVisible в 0; Intersec(r1,l) - поиск пересечения отрезка со сторонами окна при условии, что точка r1 лежит в окне; C1, C2 - коды точек r1, r2.
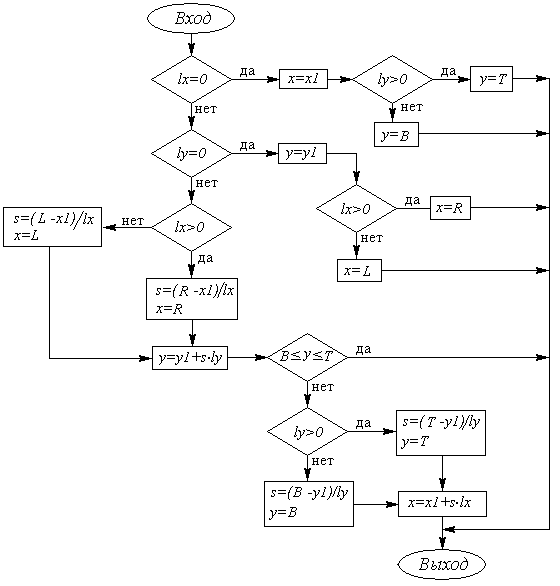
Рис. 6.2. Блок-схема алгоритма Сазерленда-Коэна В приведенном алгоритме теперь остается только детализовать функции Intersec0 и Intersec, эффективность работы которых является ключевым моментом. Рассмотрим один из методов поиска пересечений, который использует параметрическое уравнение прямой, проходящей через точки
или в координатном виде
Попробуем определить точку пересечения отрезка с верхней границей окна. Поскольку эта граница описывается соотношениями
то условие пересечения с ней клиппируемого отрезка выглядит следующим образом:
Аналогично выглядят формулы и для остальных границ окна. Если точка Этот алгоритм реализован в виде функции Intersec, блок-схема которой приведена на рис. 6.3. Теперь рассмотрим случай, когда ни один из концов отрезка не лежит внутри окна. Здесь мы можем найти первую точку пересечения, заменить ею один из концов отрезка и использовать предыдущий алгоритм нахождения второй точки. Заметим, что в данном случае первый шаг не всегда кончается успешно, поскольку предварительный анализ не позволяет полностью исключить все невидимые отрезки. Как и в предыдущем алгоритме, сначала выполняется проверка на горизонтальное и вертикальное направления отрезка. Поскольку часть отрезков мы уже исключили из рассмотрения благодаря предварительному анализу, то для этих простых ситуаций остаются только две возможности, приведенные на рис. 6.4. Здесь точки пересечения определяются совершенно очевидным образом, причем сразу обе. Затем последовательно рассматриваются четыре случая расположения точки Предложенная реализация алгоритма отсечения не является единственной в своем роде. Существуют и другие подходы, в частности использование метода деления отрезка пополам для поиска точек пересечения и выявления видимой части отрезка. Такой вариант алгоритма был предложен Сазерлендом и Спрулом для аппаратной реализации, но он может быть реализован и на программном уровне, хотя при этом эффективность его будет ниже, чем у предыдущего. В нем нет прямого вычисления координат новой точки по явным алгебраическим соотношениям. Поиск осуществляется итерационным методом, в котором на каждом шаге для отрезка, "подозреваемого" в частичной видимости, находится его средняя точка, определяется ее код, затем из двух отрезков оставляются либо оба (если они оба не окажутся полностью невидимыми), либо только один, после чего операции продолжаются с новыми отрезками. Ситуация, когда дальнейшему дроблению подвергаются сразу два вновь полученных отрезка, может возникнуть только на первом итерационном шаге в тех случаях, когда исходный отрезок имеет две точки пересечения с границами окна. На последующих итерационных шагах количество анализируемых отрезков уже не будет увеличиваться. Процесс продолжается до тех пор, пока длина очередного отрезка не станет меньше наперед заданной точности. После этого найденная точка проверяется на предмет пересечения со стороной окна. На рис. 6.6 приведены три варианта отрезков, предварительный анализ которых не классифицирует их как полностью невидимые, и показан первый итерационный шаг. Отрезок a после первого деления дает два частично видимых отрезка, после чего ищутся две точки пересечения. В остальных случаях остается лишь один из двух отрезков, причем в случае отрезка c точка пересечения со стороной окна отсутствует, т.е. обнаруживается полная невидимость отрезка. По сути дела общий алгоритм, показанный на рис. 6.3, сохраняется, изменяется лишь метод поиска точки пересечения.
Рис. 6.3. Блок-схема функции Intersec
Рис. 6.4. Отрезки параллельны сторонам окна
Рис. 6.5. Блок-схема функции Intrsec0
Рис. 6.6. Произвольное расположение отрезков
|

 , удовлетворяющих соотношениям
, удовлетворяющих соотношениям
 и
и  . Первый шаг алгоритма нацелен на то, чтобы выявить полностью видимые и полностью невидимые отрезки. Отрезок целиком принадлежит выделяемой (клиппируемой) области, если оба его конца удовлетворяют условиям (5.1).
. Первый шаг алгоритма нацелен на то, чтобы выявить полностью видимые и полностью невидимые отрезки. Отрезок целиком принадлежит выделяемой (клиппируемой) области, если оба его конца удовлетворяют условиям (5.1).
 ;
; ;
; ;
; .
. , 2-й - за прямую
, 2-й - за прямую  , 3-й - за
, 3-й - за 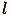 , 4-й - за
, 4-й - за  . Если в коде области какой-либо бит установлен в 1, то это означает, что она отделена от окна соответствующей прямой. Схема идентификации областей приведена на рис. 6.1.
. Если в коде области какой-либо бит установлен в 1, то это означает, что она отделена от окна соответствующей прямой. Схема идентификации областей приведена на рис. 6.1. , массив координат окна
, массив координат окна  ;
;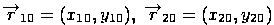 , а также значение переменной IsVisible (0 - отрезок видимый);
, а также значение переменной IsVisible (0 - отрезок видимый);
 :
:



 расположена внутри окна, то, в зависимости от знака
расположена внутри окна, то, в зависимости от знака  , следует искать пересечение либо с верхней, либо с нижней границей окна. При отсутствии таковых отыскиваются пересечения с левой или правой стороной окна. Но прежде чем перебирать эти варианты, необходимо исключить случаи горизонтальных
, следует искать пересечение либо с верхней, либо с нижней границей окна. При отсутствии таковых отыскиваются пересечения с левой или правой стороной окна. Но прежде чем перебирать эти варианты, необходимо исключить случаи горизонтальных  и вертикальных
и вертикальных  направлений отрезка. В первом случае точками пересечения с правой или левой границей (в зависимости от знака
направлений отрезка. В первом случае точками пересечения с правой или левой границей (в зависимости от знака  ) могут быть
) могут быть  или
или  , а во втором -
, а во втором -  или
или 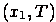 .
.