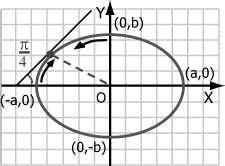
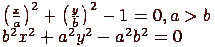Изображение эллипсов

Прежде всего отметим, что у эллипса, в отличие от окружности, всего 2 оси симметрии, поэтому по точкам придется строить уже 2 октанта (см. рис. 4.11).

Рис. 4.11. Изображение эллипса

Построение по неявной функции

Будем рассуждать подобно алгоритму Брезенхема для окружностей.

Неявная функция, задающая эллипс, имеет вид

Введем f(x, y) = b²x² + a²y² - a²b².

Аналогично алгоритму для окружности можно сравнивать f для двух возможных вариантов. Подробный вывод оставляем читателю в качестве упражнения.

Построение путем сжатия окружности

Воспользуемся тем, что эллипс с параметрами a, b (пусть a > b) получается из окружности радиуса a сжатием по оси y в a/b раз. Построим алгоритм, который является некой комбинацией алгоритмов Брезенхема для окружности и для отрезка (см. рис. 4.12).

Рис. 4.12. Построение эллипса путем сжатия окружности

Рис. 4.13. Смешанная связность

Начнем из точки (a, 0) на окружности и из точки (0, 0) на отрезке. Будем строить эллипс точно так же, как окружность, но смещать текущую точку по y только в том случае, когда такое смещение происходит в текущем шаге уже для отрезка, т.е. построение отрезка как раз и является реализацией сжатия в a/b раз (точнее, его дискретной аппроксимацией). Этот алгоритм тоже имеет недостаток: возможная смешанная связность полученной линии (см. рис. 4.13).