Матрицы. В дальнейшем будем использовать сокращенную запись для матрицы
Для выполнения преобразований векторов в пространстве мы будем использовать матричный метод. Матрицей размерности
В дальнейшем будем использовать сокращенную запись для матрицы: Сначала введем ряд операций над матрицами и векторами. Пусть заданы матрицы Определим также операцию умножения матрицы на число. Результатом умножения матрицы Произведением двух матриц
Произведение матриц некоммутативно, т.е. в общем случае Предыдущие определения мы вводили для матриц произвольной размерности. Следующие операции будут связаны с векторами, и мы будем подразумевать, что
Если матрица Аналогичным образом определяется умножение вектора на матрицу, только в этом случае вектор скалярно умножается на вектор-строки матрицы. Матрица вида
называется единичной и обладает следующими свойствами: · · · Если для матрицы · Если для матриц Благодаря операции умножения матрицы на вектор любая матрица определяет преобразование в пространстве, по которому каждому вектору сопоставляется некоторый другой по вполне определенному закону. Отметим, что для геометрических преобразований удобно использовать матрицы размерностью на единицу больше, чем размерность пространства, но об этом подробнее речь пойдет в следующей главе. Геометрические преобразования (перенос, масштабирование, вращение) Геометрические объекты на плоскости и в пространстве можно подвергать ряду различных преобразований. Наиболее употребительными в задачах компьютерной графики являются: · перемещение (параллельный перенос); · изменение размеров (масштабирование); · повороты вокруг некоторой точки на плоскости или некоторой оси в пространстве (вращение). В дальнейшем мы часто будем отождествлять точки пространства с радиус-вектором, определяемым этой точкой. Сначала рассмотрим преобразования на плоскости, или двумерные преобразования. Параллельный перенос объекта сводится к перемещению всех его точек на одно и то же расстояние Масштабирование объекта можно реализовать путем умножения координат всех его точек на некоторое число. Пусть имеются точки с координатами В случае, когда
Рис. 3.5. Масштабирование с сохранением углов
Рис. 3.6. Масштабирование с искажением углов Вращения в плоскости перемещают точки по дуге окружности, центр которой находится в начале координат. Рассмотрим сначала движение одной точки при повороте на угол
После поворота вектор будет составлять угол
Можно показать, что при таком преобразовании сохраняются расстояния между точками, а следовательно, и углы между отрезками.
Рис. 3.7. Поворот на плоскости
Рис. 3.8. Поворот в пространстве В случае трехмерного пространства рассуждения, касающиеся переноса и масштабирования, полностью аналогичны, только они распространяются на третью координату точек. С вращением же дело обстоит иначе, поскольку здесь вращательное движение есть перемещение вдоль поверхности сферы и поворот на какой-то угол относительно точки нельзя определить однозначно. Но перемещение из одной точки сферы в другую всегда можно осуществить последовательностью поворотов относительно осей координат, поэтому выведем формулы для этих трех вращений. При повороте относительно оси
Формулы поворота относительно оси
Во всех этих формулах следует обратить внимание на знаки, так как они зависят от того, какой поворот считается положительным (в данном случае мы имеем дело с правой тройкой базисных векторов). Преобразования масштабирования и поворота на плоскости и в пространстве можно выразить с помощью матриц. Если заданы коэффициенты масштабирования
Двумерный случай выглядит подобным же образом. Поворот на плоскости можно осуществить с помощью матрицы
И наконец, повороты в пространстве относительно осей координат можно выполнить с помощью трех матриц вращения
Нетрудно проверить, что для матриц вращения справедливо соотношение
Для выполнения последовательных поворотов вокруг осей на углы
Использование этой матрицы даст заметную экономию в вычислениях по сравнению с последовательными умножениями на каждую из трех матриц вращения.
|

 называется таблица чисел вида
называется таблица чисел вида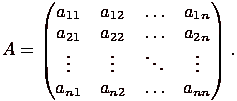
 . Строки матрицы
. Строки матрицы  будем называть вектор-строками (поскольку каждая из них определяет вектор), а столбцы
будем называть вектор-строками (поскольку каждая из них определяет вектор), а столбцы  - вектор-столбцами. Матрицы являются эффективным инструментом для выполнения преобразований на плоскости и в пространстве. В этих случаях применяются матрицы размерности
- вектор-столбцами. Матрицы являются эффективным инструментом для выполнения преобразований на плоскости и в пространстве. В этих случаях применяются матрицы размерности  и
и  .
. и
и  . Суммой матриц называется матрица
. Суммой матриц называется матрица  , элементами которой являются
, элементами которой являются  .
. на число
на число  является матрица
является матрица  .
.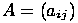 и
и  называется матрица
называется матрица  , элементы которой определяются следующим образом:
, элементы которой определяются следующим образом:
 .
. или
или 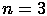 . Пусть задана матрица
. Пусть задана матрица  . Результатом умножения матрицы на вектор является вектор
. Результатом умножения матрицы на вектор является вектор  , координаты которого вычисляются как скалярное произведение строки матрицы на вектор:
, координаты которого вычисляются как скалярное произведение строки матрицы на вектор:
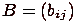 получена из матрицы
получена из матрицы  путем замены всех вектор-строк на вектор-столбцы, т.е.
путем замены всех вектор-строк на вектор-столбцы, т.е.  , то ее называют транспонированной матрицей
, то ее называют транспонированной матрицей  и обозначают
и обозначают 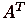 .
.
 для любой матрицы
для любой матрицы  .
. для любого вектора
для любого вектора  .
. существует матрица
существует матрица  , такая, что
, такая, что  , то
, то  . При этом
. При этом  , и для любого вектора
, и для любого вектора  получаем соотношения: если
получаем соотношения: если  , то
, то  .
. и
и  существуют обратные матрицы, то существует и обратная матрица для их произведения и
существуют обратные матрицы, то существует и обратная матрица для их произведения и  .
.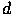 в одном и том же направлении, заданном определенным вектором
в одном и том же направлении, заданном определенным вектором  . Если этот вектор имеет длину
. Если этот вектор имеет длину 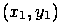 и
и  , над которыми выполняется такое преобразование. Результатом будут новые точки с координатами
, над которыми выполняется такое преобразование. Результатом будут новые точки с координатами 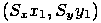 и
и  . Если
. Если 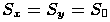 , то несложно доказать, что обе точки переместятся вдоль прямых, проходящих через саму точку и начало координат, т.е. в направлении своего же радиус-вектора (рис. 3.5). При этом расстояние между новыми точками будет в
, то несложно доказать, что обе точки переместятся вдоль прямых, проходящих через саму точку и начало координат, т.е. в направлении своего же радиус-вектора (рис. 3.5). При этом расстояние между новыми точками будет в  раз отличаться от прежнего, но углы между отрезками сохранятся (это можно показать, если выразить косинус угла через скалярное произведение векторов). Ясно, что если коэффициент масштабирования
раз отличаться от прежнего, но углы между отрезками сохранятся (это можно показать, если выразить косинус угла через скалярное произведение векторов). Ясно, что если коэффициент масштабирования  , расстояния между точками изменятся неравномерно, поскольку растяжения в горизонтальном и вертикальном направлениях будут различными. Углы между отрезками также не сохранятся (рис. 3.6).
, расстояния между точками изменятся неравномерно, поскольку растяжения в горизонтальном и вертикальном направлениях будут различными. Углы между отрезками также не сохранятся (рис. 3.6).
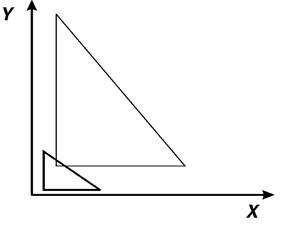
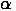 (положительным является направление против часовой стрелки), т. е. поворот радиус-вектора на угол (рис. 3.7). Пусть точка располагалась на расстоянии
(положительным является направление против часовой стрелки), т. е. поворот радиус-вектора на угол (рис. 3.7). Пусть точка располагалась на расстоянии  от начала координат, а ее радиус-вектор составлял угол
от начала координат, а ее радиус-вектор составлял угол 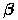 с осью абсцисс. Тогда координаты точки определяются формулами
с осью абсцисс. Тогда координаты точки определяются формулами
 , а новые координаты точки будут определяться соотношениями
, а новые координаты точки будут определяться соотношениями


 на угол
на угол  остается неизменной. Если смотреть на плоскость
остается неизменной. Если смотреть на плоскость  со стороны конца оси
со стороны конца оси  к оси
к оси  . Если воспользоваться формулами для плоских поворотов, то координаты
. Если воспользоваться формулами для плоских поворотов, то координаты  и
и  новой точки определяются выражениями
новой точки определяются выражениями
 полностью совпадают с теми, которые были выведены для плоского случая, а поворот относительно оси
полностью совпадают с теми, которые были выведены для плоского случая, а поворот относительно оси 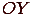 выглядит так:
выглядит так:
 , то преобразование точки осуществляется посредством умножения матрицы на ее радиус-вектор,
, то преобразование точки осуществляется посредством умножения матрицы на ее радиус-вектор,



 можно создать матрицу преобразования путем перемножения трех матриц:
можно создать матрицу преобразования путем перемножения трех матриц:



