Уравнения прямой и плоскости
Уравнение прямой на плоскости в декартовой системе координат можно задать уравнением вида
для случая, когда прямая не параллельна оси OY, и уравнением
для вертикальной прямой. Но прямая может быть также задана и другим способом. Достаточно указать вектор направления этой прямой
в котором параметр t пробегает все значения числовой прямой. Координаты точки, соответствующей некоторому значению этого параметра, определяются соотношениями
Прямую в пространстве тоже можно задавать параметрическим уравнением, которое очень легко получить из предыдущего простым переходом от двумерных векторов к трехмерным. Пусть
Как известно из элементарной геометрии, через любые три точки в пространстве проходит плоскость. С другой стороны, через каждую точку плоскости можно провести единственную прямую, перпендикулярную данной плоскости. При этом все эти прямые будут параллельны друг другу, а значит, они имеют общий вектор направления. Этот вектор будем называть нормалью к плоскости. Если длина вектора равна единице, мы будем называть его единичной нормалью. В компьютерной графике часто приходится решать задачу построения нормали к некоторой плоскости, заданной тремя точками, а также задачи пересечения прямой с плоскостью и двух плоскостей. Плоскость в пространстве можно задать, указав вектор нормали к ней и какую-либо точку, принадлежащую данной плоскости. Пусть
Раскрывая это выражение в координатном виде, получаем
Теперь перепишем это уравнение в виде
где В алгоритмах компьютерной графики довольно часто приходится сталкиваться с задачей построения плоскости, проходящей через три заданные точки. Пусть три точки
Остается определить значение
следовательно
и после подстановки окончательно получим:
В большинстве алгоритмов, использующих плоскости, достаточно знать нормаль к ней и какую-либо точку, принадлежащую плоскости. Очевидно, что по аналогии можно вывести каноническое уравнение прямой на плоскости, если задана нормаль к ней и принадлежащая прямой точка.
|



 и какую-нибудь точку
и какую-нибудь точку  , лежащую на этой прямой. При этом точки, лежащие на прямой, могут быть заданы с использованием векторных операций в виде так называемого параметрического уравнения прямой
, лежащую на этой прямой. При этом точки, лежащие на прямой, могут быть заданы с использованием векторных операций в виде так называемого параметрического уравнения прямой

 . Тогда это уравнение будет определять прямую в пространстве, а координаты точек этой прямой будут определяться формулами
. Тогда это уравнение будет определять прямую в пространстве, а координаты точек этой прямой будут определяться формулами
 - вектор единичной нормали, а
- вектор единичной нормали, а  - некоторая точка на плоскости. Тогда для любой точки
- некоторая точка на плоскости. Тогда для любой точки  , лежащей на плоскости, вектор
, лежащей на плоскости, вектор  будет ортогонален вектору нормали, а следовательно, выполняется равенство
будет ортогонален вектору нормали, а следовательно, выполняется равенство


 . Это уравнение называется каноническим уравнением плоскости. При этом совершенно ясно, что если все это уравнение умножить на какой-либо отличный от нуля множитель, то оно будет описывать ту же самую плоскость, т.е. коэффициенты
. Это уравнение называется каноническим уравнением плоскости. При этом совершенно ясно, что если все это уравнение умножить на какой-либо отличный от нуля множитель, то оно будет описывать ту же самую плоскость, т.е. коэффициенты  для каждой плоскости задаются с точностью до произвольного ненулевого множителя. Но если при этом вектор
для каждой плоскости задаются с точностью до произвольного ненулевого множителя. Но если при этом вектор  имеет единичную длину, то
имеет единичную длину, то  задает расстояние от начала координат до данной плоскости.
задает расстояние от начала координат до данной плоскости. ,
,  и
и 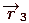 , не лежащие на одной прямой, имеют координатами
, не лежащие на одной прямой, имеют координатами 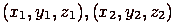 и
и  . Для канонического уравнения необходимо построить нормаль к плоскости, что легко можно осуществить, используя операцию векторного произведения. Поскольку векторы
. Для канонического уравнения необходимо построить нормаль к плоскости, что легко можно осуществить, используя операцию векторного произведения. Поскольку векторы  и
и  лежат в искомой плоскости, то вектор
лежат в искомой плоскости, то вектор  будет ортогонален этой плоскости. Пусть
будет ортогонален этой плоскости. Пусть  , тогда уравнение плоскости будет иметь вид
, тогда уравнение плоскости будет иметь вид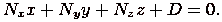
 . Так как точка
. Так как точка  принадлежит этой плоскости, то ее координаты должны удовлетворять полученному уравнению. Подставим их в уравнение и получим
принадлежит этой плоскости, то ее координаты должны удовлетворять полученному уравнению. Подставим их в уравнение и получим