Цветовой график МКО
Трехмерная природа восприятия цвета позволяет отображать его в прямоугольной системе координат. Любой цвет можно изобразить в виде вектора, компонентами которого являются относительные веса красного, зеленого и синего цветов, вычисленные по формулам
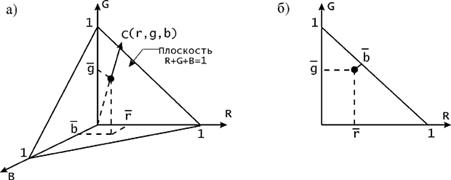
Поскольку эти координаты в сумме всегда составляют единицу, а каждая из координат лежит в диапазоне от 0 до 1, то все представленные таким образом точки пространства будут лежать в одной плоскости, причем только в треугольнике, отсекаемом от нее положительным октантом системы координат (рис. 2.5а). Ясно, что при таком представлении все множество точек этого треугольника можно описать с помощью двух координат, так как третья выражается через них посредством соотношения
Таким образом, мы переходим к двумерному представлению области, т.е. к проекции области на плоскость (рис. 2.5б).
Рис. 2.5. Трехмерное цветовое пространство С использованием такого преобразования в 1931 г. были выработаны международные стандарты определения и измерения цветов. Основой стандарта стал так называемый двумерный цветовой график МКО. Поскольку, как показали физические эксперименты, сложением трех основных цветов можно получить не все возможные цветовые оттенки, то в качестве базисных были выбраны другие параметры, полученные на основе исследования стандартных реакций глаза на свет. Эти параметры -
При проекции этого треугольника на плоскость получается цветовой график МКО. Но координаты цветности определяют только относительные количества основных цветов, не задавая яркости результирующего цвета. Яркость можно задать координатой
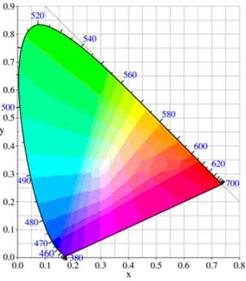
Рис. 2.6. Цветовой график МКО. На контуре указаны длины волн в нанометрах Цветовой график МКО приведен на рис. 2.6. Область, ограниченная кривой, охватывает весь видимый спектр, а сама кривая называется линией спектральных цветностей. Числа, проставленные на рисунке, означают длину волны в соответствующей точке. Точка Цветовой график удобен для целого ряда задач. Например, с его помощью можно получить дополнительный цвет: для этого надо провести луч от данного цвета через опорную точку до пересечения с другой стороной кривой (цвета являются дополнительными друг к другу, если при сложении их в соответствующей пропорции получается белый цвет). Для определения доминирующей длины волны какого-либо цвета также проводится луч из опорной точки до пересечения с данным цветом и продолжается до пересечения с ближайшей точкой линии цветностей. Для смешения двух цветов используются законы Грассмана. Пусть два цвета заданы на графике МКО координатами
Координаты МКО являются точным стандартом определения цвета. Но в различных областях, имеющих дело с цветом, есть свой подход к его моделированию. В частности, может использоваться другой набор основных цветов. Компьютерная графика опирается на систему
|

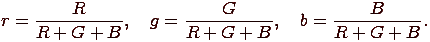
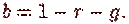
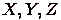 - являются чисто теоретическими, поскольку построены с использованием отрицательных значений основных составляющих цвета. Треугольник основных цветов был построен так, чтобы охватывать весь спектр видимого света. Кроме того, равное количество всех трех гипотетических цветов в сумме дает белый цвет. Координаты цветности строятся так же, как и в приведенной выше формуле:
- являются чисто теоретическими, поскольку построены с использованием отрицательных значений основных составляющих цвета. Треугольник основных цветов был построен так, чтобы охватывать весь спектр видимого света. Кроме того, равное количество всех трех гипотетических цветов в сумме дает белый цвет. Координаты цветности строятся так же, как и в приведенной выше формуле:
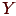 , а
, а 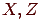 определить исходя из величин
определить исходя из величин 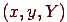 , по формулам
, по формулам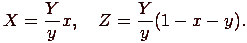
 , соответствующая полуденному освещению при сплошной облачности, принята в качестве опорного белого цвета.
, соответствующая полуденному освещению при сплошной облачности, принята в качестве опорного белого цвета.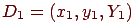 и
и 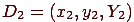 . Тогда смешение их дает цвет
. Тогда смешение их дает цвет 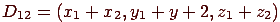 . Если ввести обозначения
. Если ввести обозначения 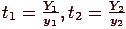 , то получим координаты цветности смеси
, то получим координаты цветности смеси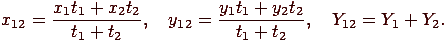
 , поэтому представляет интерес переход между этими двумя наборами цветов (иными словами, преобразование координат цветности).
, поэтому представляет интерес переход между этими двумя наборами цветов (иными словами, преобразование координат цветности).


