Системы координат и векторы
Для дальнейшего изложения нам понадобятся некоторые сведения из аналитической геометрии и линейной алгебры. Не ставя перед собой задачу подробного рассмотрения всех этих вопросов, приведем (или напомним) те основные понятия и операции, которые используются в алгоритмах компьютерной графики. Две взаимно перпендикулярные пересекающиеся прямые с заданным масштабом образуют декартову прямоугольную систему координат на плоскости. Точка пересечения O называется началом координат, прямые называются осями координат. Одну из осей называют осью OX, или осью абсцисс, другую - осью OY, или осью ординат. Эти оси также называют координатными осями. Возьмем произвольную точку Три взаимно перпендикулярные пересекающиеся прямые с заданным масштабом образуют декартову прямоугольную систему координат в пространстве. Так же как и в случае плоскости, точка пересечения O называется началом координат, прямые называются осями координат. Одну из осей называют осью OX, или осью абсцисс, другую - осью OY, или осью ординат, третью - осью OZ, или осью аппликат. Пусть
Рис. 3.1. Система координат на плоскости Пусть на плоскости задана декартова система координат. Возьмем две точки с координатами
Расстояние между двумя точками в пространстве с координатами
Рис. 3.2. Система координат в пространстве Отрезок на плоскости и в пространстве задается с помощью двух точек, указывающих его границы. Геометрическим вектором, или просто вектором в пространстве, будем называть отрезок, у которого указано, какая из его граничных точек является началом, а какая - концом (т.е. указано направление вектора). Начало вектора называют точкой его приложения. Вектор называется нулевым, если его начало и конец совпадают. Векторы называются коллинеарными, если они лежат на параллельных прямых. Векторы считаются равными, если они коллинеарны, имеют одинаковую длину и одинаковое направление. Таким образом, все векторы, получающиеся параллельным переносом из одного и того же вектора, равны мeжду собой. Любая точка на плоскости и в пространстве может рассматриваться как вектор, начало которого совпадает с началом координат (радиус-вектор), а каждый вектор, перенесенный в начало координат, задает своим концом единственную точку пространства. Поэтому любой вектор может быть представлен совокупностью своих координат в декартовой системе. Линейными операциями над векторами принято называть операции сложения векторов и операцию умножения вектора на число. Суммой двух векторов Перечислим основные свойства операции сложения векторов:
Разностью двух векторов Произведением Операция умножения вектора на число обладает следующими свойствами:
Линейной комбинацией векторов Если два вектора
Векторы Векторы называются линейно независимыми, если равенство нулю их линейной комбинации возможно только в случае равенства нулю коэффициентов Справедливы следующие свойства:
Говорят, что пара линейно независимых векторов на плоскости (тройка линейно независимых векторов в пространстве) образуют базис, поскольку любой вектор может быть представлен в виде линейной комбинации этих векторов. Коэффициенты разложения вектора по базисным векторам называются координатами вектора в этом базисе. Если векторы базиса взаимно перпендикулярны и имеют единичную длину, то базис называется ортонормированным, а векторы базиса называются ортами. Таким образом, базис из единичных векторов, направленных вдоль осей декартовой системы координат, является ортонормированным. Скалярным произведением векторов
Несложно доказать следующие свойства данной операции.
Приведем некоторые формулы, связанные с разложением вектора в декартовой системе координат. Пусть векторы
Отсюда следует условие перпендикулярности векторов:
И, наконец, косинус угла между векторами вычисляется по формуле
Теперь расстояние между двумя точками с координатами
Введем еще одно понятие, касающееся векторов. Три вектора называются упорядоченной тройкой, если указано, какой из этих векторов является первым, какой - вторым и какой - третьим. При записи тройки векторов будем располагать эти векторы в порядке их следования. Так, запись Тройка векторов называется правой (левой), если после приведения к общему началу вектор Векторным произведением вектора · длина вектора · вектор · вектор Приведем (без доказательства) основные свойства векторного произведения.
Ясно, что векторное произведение двух коллинеарных векторов дает нулевой вектор. Выведем теперь формулу для векторного произведения. Пусть базисные векторы декартовой системы координат
Если заданы два вектора
где
|

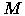 на плоскости с заданной системой координат. Пусть
на плоскости с заданной системой координат. Пусть 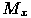 и
и  - проекции этой точки на оси абсцисс и ординат соответственно, причем длина отрезка
- проекции этой точки на оси абсцисс и ординат соответственно, причем длина отрезка  равна
равна  , а длина
, а длина 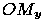 равна
равна 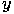 . Тогда пара чисел
. Тогда пара чисел 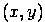 называется декартовыми координатами точки
называется декартовыми координатами точки 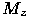 - проекции произвольной точки
- проекции произвольной точки  равна
равна  . Тогда тройка чисел
. Тогда тройка чисел  называется декартовыми координатами точки
называется декартовыми координатами точки 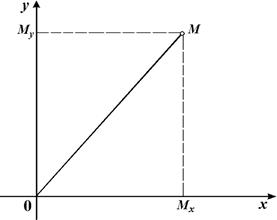
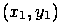 и
и  соответственно. Тогда, используя терему Пифагора, можно получить, что расстояние между этими двумя точками выражается формулой
соответственно. Тогда, используя терему Пифагора, можно получить, что расстояние между этими двумя точками выражается формулой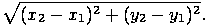
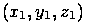 и
и  выражается аналогичной формулой:
выражается аналогичной формулой: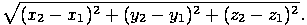

 и
и 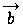 называется вектор, идущий из начала вектора
называется вектор, идущий из начала вектора 
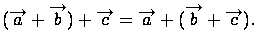
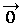 , такой, что
, такой, что 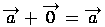 для любого вектора
для любого вектора  , такой, что
, такой, что 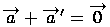 .
.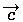 , который в сумме с вектором
, который в сумме с вектором 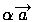 вектора
вектора  называется вектор
называется вектор  и направление, совпадающее с направлением вектора
и направление, совпадающее с направлением вектора  и противоположное направлению
и противоположное направлению  . Геометрический смысл умножения вектора на число состоит в том, что длина вектора увеличивается в
. Геометрический смысл умножения вектора на число состоит в том, что длина вектора увеличивается в  раз.
раз. (распределительное свойство числового сомножителя относительно суммы векторов);
(распределительное свойство числового сомножителя относительно суммы векторов); (распределительное свойство векторного сомножителя относительно суммы чисел);
(распределительное свойство векторного сомножителя относительно суммы чисел);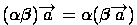 (сочетательное свойство числовых сомножителей);
(сочетательное свойство числовых сомножителей);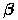 , такое, что
, такое, что  .
.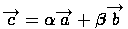 . При этом числа
. При этом числа 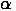 и
и  и
и  заданы своими координатами
заданы своими координатами  и
и  , то операции над ними легко выразить через эти координаты:
, то операции над ними легко выразить через эти координаты:


 существуют числа
существуют числа  , такие, что
, такие, что 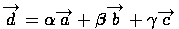 , причем эта тройка чисел для каждого вектора - единственная (разложение вектора
, причем эта тройка чисел для каждого вектора - единственная (разложение вектора 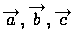 ).
). . Тогда скалярное произведение можно выразить формулой
. Тогда скалярное произведение можно выразить формулой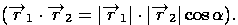
 (свойство коммутативности).
(свойство коммутативности). (сочетательное относительно числового множителя свойство).
(сочетательное относительно числового множителя свойство). (распределительное относительно суммы векторов свойство).
(распределительное относительно суммы векторов свойство).

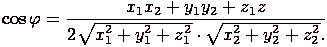
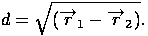
 означает, что первым вектором тройки является вектор
означает, что первым вектором тройки является вектор  и удовлетворяющий следующим требованиям:
и удовлетворяющий следующим требованиям:
 направлен так, что тройка векторов
направлен так, что тройка векторов  является правой.
является правой. (антисимметричность);
(антисимметричность); (сочетательное свойство относительно умножения на число);
(сочетательное свойство относительно умножения на число); (распределительное свойство относительно сложения);
(распределительное свойство относительно сложения); для любого вектора
для любого вектора  .
. образуют правую тройку. Тогда справедливы следующие соотношения:
образуют правую тройку. Тогда справедливы следующие соотношения:
 и
и 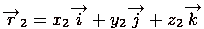 , то, учитывая свойства векторного произведения, отсюда легко вывести, что
, то, учитывая свойства векторного произведения, отсюда легко вывести, что