Изображение отрезка с нецелочисленными координатами концовДля отрезка с нецелочисленными координатами концов будем строить соответствующую 4-связную линию на растре.
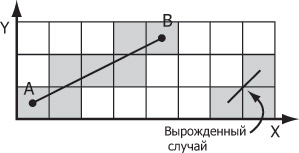
Рис. 4.5. Рисование отрезка с нецелочисленными координатами концов. Существует два подхода.
где A и B - концевые точки, c > 0 - некий масштабный коэффициент. Сделаем c достаточно большим целым числом, чтобы уменьшить ошибки округления. Тогда рассмотрим
- приращение t, при сдвиге на 1 пиксель по x;
- приращение t, при сдвиге на 1 пиксель по y. Будем сравнивать текущие значения h и v, а затем, в зависимости от этого, делать шаг по x или y и придавать соответствующие приращения h и v. Алгоритм закончится, когда h или v превысит c.
Рис. 4.6. Изменение параметров h и v x = 0; y = 0; // Канонический случай: начальная точка// лежит в [0, 1) [0, 1) /* Приращения t, соответствующие смещениям от начальнойточки до границ первого пикселя. */ h = Δh * (1 - xA); // Δh0v = Δv * (1 - yA); // Δv0 while((h < c) AND (v < c)){ plot(x, y); if(h < v) { // Сдвиг по горизонтали x++; h += Δh; } else if(h > v) { // Сдвиг по вертикали y++; v += Δv; } else { // h = v: Вырожденный случай (см. рис. 3.5) // рисуем произвольный из двух возможных пикселей, // например, верхний: plot(x,y+1); x++; y++; h += Δh; v += Δv; }} Листинг 4.4. Алгоритм отображения отрезка с нецелочисленными координатами концов Замечание. Приведенный выше алгоритм легко обобщается на n-мерный случай.
|
в этом случае: 
. Параметризуем наш отрезок стандартным образом: 
