Отсечение выпуклым многоугольником
Во многих задачах компьютерной графики часто приходится иметь дело с отсечением не только простым прямоугольным окном, но и окном достаточно произвольной геометрии. В частности, такие задачи могут возникнуть при использовании перспективных проекций трехмерных сцен, но не только в этих случаях. Поэтому актуальной является задача отсечения выпуклым многоугольником. Ясно, что простой анализ с помощью кодов Сазерленда-Коэна в такой ситуации неприменим. Здесь нужен надежный и достаточно эффективный алгоритм нахождения точки пересечения двух произвольно ориентированных отрезков, а также алгоритм определения местоположения точки относительно многоугольника (внутри, снаружи или на границе). Рассмотрим задачу о пересечении отрезка с концами
Рис. 6.7. Пересечение отрезка многоугольником Конечно, использование этой формулы предполагает, что Для каждого отрезка возможны три случая взаимного расположения с многоугольником:
В каждом из этих вариантов для нахождения пересечения отрезка с окном необходимо уметь определять принадлежность точки выпуклому многоугольнику. Из рис. 6.7 видно, что если для любой точки Таким образом, алгоритм отсечения отрезка начинается с анализа расположения концов отрезка по отношению к окну. Если обе точки лежат внутри окна, то отрезок полностью видимый, и дальнейший поиск прекращается. Если только одна из точек лежит внутри окна, то имеет место случай II, и предстоит найти одну точку пересечения. И, наконец, если обе точки лежат вне окна, то существуют либо две точки пересечения (отрезок пересекает две границы окна), либо ни одной (отрезок полностью невидим). Впрочем, две точки пересечения могут совпадать (если отрезок проходит через вершину многоугольника), но этот случай в дополнительном анализе не нуждается. Далее выполняется цикл по всем ребрам многоугольника с целью нахождения точек пересечения. Для каждого ребра перед началом поиска пересечения необходимо проверить, не параллельно ли оно с отрезком. Если это так, то можно вычислить расстояние от одного из концов отрезка до прямой, проходящей через ребро
|

 с выпуклым многоугольником, заданным списком ребер. Ребро может быть задано в виде пары точек из множества вершин многоугольника
с выпуклым многоугольником, заданным списком ребер. Ребро может быть задано в виде пары точек из множества вершин многоугольника  (рис. 6.7). То обстоятельство, что многоугольник выпуклый, является очень существенным: это позволяет использовать достаточно простой алгоритм, использующий внутренние нормали к его сторонам. Под внутренней нормалью понимается вектор, перпендикулярный стороне и направленный внутрь многоугольника. Как и в предыдущем алгоритме, воспользуемся параметрическим уравнением прямой, проходящей через концы отрезка:
(рис. 6.7). То обстоятельство, что многоугольник выпуклый, является очень существенным: это позволяет использовать достаточно простой алгоритм, использующий внутренние нормали к его сторонам. Под внутренней нормалью понимается вектор, перпендикулярный стороне и направленный внутрь многоугольника. Как и в предыдущем алгоритме, воспользуемся параметрическим уравнением прямой, проходящей через концы отрезка:  . Если при некотором значении параметра
. Если при некотором значении параметра  эта прямая пересекается с прямой, проходящей через точки
эта прямая пересекается с прямой, проходящей через точки  , то вектор, соединяющий произвольную точку ребра с точкой
, то вектор, соединяющий произвольную точку ребра с точкой  , будет перпендикулярен вектору нормали. Следовательно, скалярное произведение векторов
, будет перпендикулярен вектору нормали. Следовательно, скалярное произведение векторов  и
и  будет равно нулю. Отсюда путем несложных выкладок получаем
будет равно нулю. Отсюда путем несложных выкладок получаем .
.
 , т.е. что отрезок не параллелен стороне многоугольника, но этот случай рассматривается отдельно. Найденная точка принадлежит отрезку при условии
, т.е. что отрезок не параллелен стороне многоугольника, но этот случай рассматривается отдельно. Найденная точка принадлежит отрезку при условии  . Условие принадлежности этой точки ребру многоугольника также можно выразить через скалярное произведение, так как векторы
. Условие принадлежности этой точки ребру многоугольника также можно выразить через скалярное произведение, так как векторы  и
и  в этом случае должны быть одинаково направленными, т.е.
в этом случае должны быть одинаково направленными, т.е.  .
. , принадлежащей многоугольнику (или его границе), и произвольной точки ребра
, принадлежащей многоугольнику (или его границе), и произвольной точки ребра  построить вектор
построить вектор  , то выполняется условие
, то выполняется условие 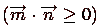 , поскольку угол между векторами не может превышать 90°. Таким образом, если данное условие выполняется для всех ребер многоугольника, то точка является внутренней.
, поскольку угол между векторами не может превышать 90°. Таким образом, если данное условие выполняется для всех ребер многоугольника, то точка является внутренней. . При
. При  отрезок лежит на прямой, и остается определить взаимное расположение концов отрезка и концов ребра, что можно сделать простым покоординатным сравнением. При
отрезок лежит на прямой, и остается определить взаимное расположение концов отрезка и концов ребра, что можно сделать простым покоординатным сравнением. При  отрезок не имеет общих точек с данным ребром.
отрезок не имеет общих точек с данным ребром.


