Кривая БезьеКривы́е Безье́ были разработаны в 60-х годах XX века независимо друг от друга Пьером Безье (Bézier) из автомобилестроительной компании «Рено» и Полем де Кастелье (de Casteljau) из компании «Ситроен», где применялись для проектирования кузовов автомобилей. Несмотря на то, что открытие де Кастелье было сделано несколько ранее Безье (1959), его исследования не публиковались и скрывались компанией как производственная тайна до конца 1960-х. Впервые кривые были представлены широкой публике в 1962 году французским инженером Пьером Безье, который, разработав их независимо от де Кастелье, использовал их для компьютерного проектирования автомобильных кузовов. Кривые были названы именем Безье, а именем де Кастелье назван разработанный им рекурсивный способ определения кривых (алгоритм де Кастелье). Впоследствии это открытие стало одним из важнейших инструментов систем автоматизированного проектирования и программ компьютерной графики. Кривая Безье — параметрическая кривая, задаваемая выражением
где
Рассмотрим кубически кривые Безье, как частный случай.
В параметрической форме кубическая кривая Безье (n = 3) описывается следующим уравнением:
Четыре опорные точки P0, P1, P2 и P3, заданные в 2-х или 3-мерном пространстве определяют форму кривой. Линия берёт начало из точки P0 направляясь к P1 и заканчивается в точке P3 подходя к ней со стороны P2. То есть кривая не проходит через точки P1 и P2, они используются для указания её направления. Длина отрезка между P0 и P1 определяет, как скоро кривая повернёт к P3. В матричной форме кубическая кривая Безье записывается следующим образом:
где
Применение в компьютерной графике Благодаря простоте задания и манипуляции, кривые Безье нашли широкое применение в компьютерной графике для моделирования гладких линий. Кривая целиком лежит в выпуклой оболочке своих опорных точек. Это свойство кривых Безье с одной стороны значительно облегчает задачу нахождения точек пересечения кривых (если не пересекаются выпуклые оболочки, то не пересекаются и сами кривые), а с другой стороны позволяет визуализировать кривую с помощью её опорных точек. Кроме того аффинные преобразования кривой (перенос, масштабирование, вращение) также могут быть осуществлены путём применения соответствующих трансформаций к опорным точкам. Наибольшее значение имеют кривые Безье второй и третьей степеней (квадратичные и кубические). Кривые высших степеней при обработке требуют большего объёма вычислений и для практических целей используются реже. Для построения сложных по форме линий отдельные кривые Безье могут быть последовательно соединены друг с другом в сплайн Безье. Для того, чтобы обеспечить гладкость линии в месте соединения двух кривых, смежные опорные точки обеих кривых должны лежать на одной линии. В программах векторной графики наподобие Adobe Illustrator или Inkscape подобные фрагменты известны под названием «путей» (path).
using System; using System.Collections.Generic; using System.ComponentModel; using System.Data; using System.Drawing; using System.Linq; using System.Text; using System.Windows.Forms;
namespace HomeWork { public partial class Form1: Form {
public Form1() { InitializeComponent(); } Bitmap bmp; int count = 0; Graphics Gr; Int32 Draww; private void Clear() { Draww = 0; bmp = new Bitmap(3000, 3000); Gr = Graphics.FromImage(bmp); Gr.Clear(Color.White); this.timer1.Enabled = false; this.pictureBox1.Image = bmp; count = 0; }
private void button1_Click(object sender, EventArgs e) { Clear(); }
private void Form1_Load(object sender, EventArgs e) { Clear(); }
private void button2_Click(object sender, EventArgs e) { }
private void pictureBox1_MouseMove(object sender, MouseEventArgs e) { this.Text = "x=" + e.X + " y=" + e.Y; if (ClickedPoint!= -1) { ppp[ClickedPoint].x = e.X; ppp[ClickedPoint].y = e.Y; } } void ert() {
}
POINT[] ppp = new POINT[1000]; private void button4_Click(object sender, EventArgs e) { for (int i = 0; i < count; i++) { } this.timer1.Enabled = true; Draww = 1; } struct POINT { public Int32 x; public Int32 y; } /// <summary> /// Функция, вычисляющая значение х и у координат точки на кривой. /// Принимает в качестве параметров вектор-массив точек и /// параметр t, характеризующий положение на кривой. /// </summary> POINT CalcBezierCurve(POINT[] pts1, Double t) { int i, c;
POINT[] pts = new POINT[count + 2]; for (int id = 0; id < count; id++) pts[id] = pts1[id];
Double p; POINT np;
c = 1; for (i = 0; i < count; i++) { pts[i].x = pts[i].x * c; pts[i].y = pts[i].y * c; c = (count - i - 1) * c / (i + 1); } p = 1; for (i = 0; i < count; i++) { pts[i].x = Convert.ToInt32(pts[i].x * p); pts[i].y = Convert.ToInt32(pts[i].y * p); p = p * t; } p = 1; for (i = count - 1; i >= 0; i--) { pts[i].x = Convert.ToInt32(pts[i].x * p); pts[i].y = Convert.ToInt32(pts[i].y * p); p = p * (1 - t); } np.x = 0; np.y = 0; for (i = 0; i < count; i++) { np.x = np.x + pts[i].x; np.y = np.y + pts[i].y; } return np;
}
///<summary> /// Процедура отрисовки кривой Безье. /// Принимает в качестве параметров дескриптор контекста устройства и /// вектор-массив точек, по которым ведется построение кривой. /// </summary> void DrawBezier(POINT[] pts) { POINT np; np.x = 0; np.y = 0; Pen p1 = new Pen(Color.FromArgb(0, 10, 170)); for (int i = 0; i < count - 1; i++) { Gr.DrawLine(p1, pts[i].x, pts[i].y, pts[(i + 1) % count].x, pts[(i + 1) % count].y); } p1 = new Pen(Color.FromArgb(200, 50, 10)); POINT lp; lp = pts[0]; for (double tt = 0.0; tt < 1.0; tt += 0.02) { np = CalcBezierCurve(pts, tt); Gr.DrawLine(p1, lp.x, lp.y, np.x, np.y); lp = np; }
Brush r = new SolidBrush(Color.White); p1.Color = Color.Black; for (int i = 0; i < count; i++) { Gr.FillEllipse(r, pts[i].x - 2, pts[i].y - 3, 6, 6); Gr.DrawEllipse(p1, pts[i].x - 3, pts[i].y - 3, 6, 6); }
}
private void pictureBox1_Click(object sender, EventArgs e) {
} Int32 ClickedPoint; private void pictureBox1_MouseDown(object sender, MouseEventArgs e) { if (Draww == 0) { ppp[count].x = e.X; ppp[count].y = e.Y; count++; Pen p1 = new Pen(Color.Black); Brush r = new SolidBrush(Color.White); Gr.FillEllipse(r, e.X - 3, e.Y - 3, 6, 6); Gr.DrawEllipse(p1, e.X - 3, e.Y - 3, 6, 6); this.pictureBox1.Image = bmp; } else { ClickedPoint = GetNumberOfPoint(e.X, e.Y, ppp);
} } private void button3_Click(object sender, EventArgs e) { bmp = new Bitmap(500, 500); Gr = Graphics.FromImage(bmp);
Pen p1 = new Pen(Color.FromArgb(0, 10, 170)); Gr.DrawEllipse(p1, 0, 0, 15, 15); this.pictureBox1.Image = bmp; }
private void timer1_Tick(object sender, EventArgs e) { Gr.Clear(Color.White); DrawBezier(ppp); this.pictureBox1.Image = bmp; } ///<summary> /// Функция, возвращающая номер точки массива, /// по которой пользователь щелкает мышью. /// Принимает в качестве параметров х и у координаты точки щелчка /// и вектор-массив точек, задающих кривую. /// </summary> int GetNumberOfPoint(int x, int y, POINT[] P) {
for (int i = 0; i < count; i++) { if ((x > P[i].x - 10 && x < P[i].x + 10) && (y > P[i].y - 10 && y < P[i].y + 10)) return i; } return -1; }
private void pictureBox1_MouseUp(object sender, MouseEventArgs e) { ClickedPoint = -1;
}
} }
|
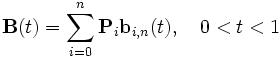
— функция компонент векторов опорных вершин, а 
— базисные функции кривой Безье, называемые также полиномами Бернштейна.
называется базисной матрицей Безье:
