Кривые Гильберта

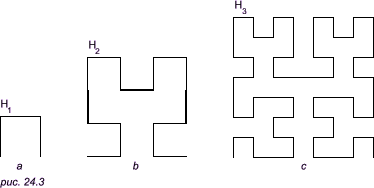
Рекурсия может быть использована для получения линейного рисунка, известного под названием кривая Гильберта. Кривая Гильберта основана на изображении буквы П, вычерченной в виде трех сторон квадрата, как показано на рис. 24.3a. Существуют кривые Гильберта порядков 1, 2,..., обозначаемые как H₁, H₂,... На рис. 24.3b изображена кривая порядка H₂, в которой некоторые отрезки прямых линий вычерчены в виде толстых линий. Это так называемые связки (в действительности связки должны иметь одинаковую толщину с другими отрезками, здесь же они показаны утолщенными единственно с целью демонстрации способа получения H₂ из H₁).

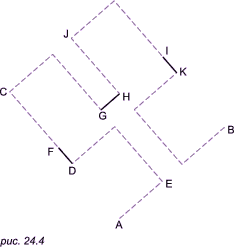
Видно, что H₂ можно рассматривать как большую букву П, четыре части которой заменены меньшими по размеру буквами П. Эти меньшие буквы П соединены тремя связками. Каждая сторона меньшей буквы П имеет ту же длину, что и связка, они в три раза меньше стороны квадрата, в который вписывается H₂. Применим ту же процедуру к каждой из четырех букв П, составляющих H₂, то есть каждую букву П в H₂ заменим меньшей H₂, одновременно уменьшим длину связок так, чтобы их длины стали равными длине элементарного отрезка прямой линии, которые содержатся в трех малых фигурах H₂. Таким образом мы получим фигуру H₃, показанную на рис. 24.3с.

Теперь все элементарные отрезки в семь раз меньше, чем длина сторон квадрата, в который вписывается фигура H₃. Отсюда получаем, что коэффициенты уменьшения для этих элементарных отрезков в фигурах H₁, H₂, H₃,... образуют ряд чисел: 1, 3, 7,..., то есть в общем случае коэффициент уменьшения для фигуры H_n может быть вычислен по формуле: 2ⁿ - 1.

Заметим, что связки в фигуре H₂ вычерчиваются в тех же направлениях, как и три отрезка, образующие букву П в фигуре H₁. При желании эти последние отрезки прямых линий можно рассматривать как связки, соединяющие четыре точки, которые в свою очередь можно принять за кривую Гильберта нулевого порядка.

В нашей программе HILBERT для построения кривых Гильберта используется рекурсивная функция hilbert со следующими аргументами: координаты точек A, B, C (см. рис. 24.4); горизонтальные и вертикальные компоненты двух направленных связок, причем одна лежит на отрезке AB, а другая — на AC. Они задаются в виде векторов, то есть как пара чисел (dx, dy), где переменные dx и dy могут принимать положительные, нулевые или отрицательные значения, в зависимости от относительного положения точек A, B и C. Эти два вектора в программе обозначаются как dAB и dAC; n — глубина рекурсии, для n = 0 функция ничего не будет делать.

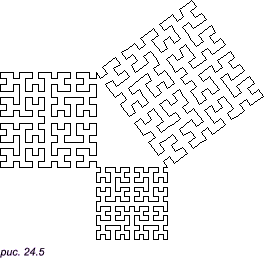
Будем считать, что рис. 24.4 является вариацией изображения буквы П (повернутой на угол 30^o против часовой стрелки), позиция которой целиком определяется тремя заданными точками A, B и C. Будем считать, что точка A является начальной точкой, а точка B — конечной. Основной причиной задания точки C является необходимость указания, с какой стороны от направленного отрезка AB должна лежать вычерчиваемая кривая. Оба заданных вектора связок dAB и dAC отмечены на рисунке в виде связок в трех местах, а именно как отрезки DF, GH и IK. Три заданные точки A, B, C и два заданных вектора dAB и dAC позволяют определить позиции точек D, E, F, G, H, I, J, K на рисунке. (Мы не будем требовать, чтобы угол CAB был прямым углом или чтобы длина отрезка AB совпадала с длиной отрезка AC, поэтому вместо квадрата каждая буква П может иметь форму произвольного параллелограмма). В общем случае пунктирные линии, показанные на рис. 24.4, фактически не вычерчиваются. Вместо этого мы будем выполнять рекурсивное обращение к нашей функции hilbert для каждой из четырех точечных букв П на рисунке. Для вычерчивания на экране трех отрезков связок DF, GH и IK будем обращаться к нашей функции draw.

На рис. 24.5 представлен результат работы программы.