Уравнения прямой в пространстве
Эпифеноменальный -сопутствующий Эшелонирование – создание интервалов Так как каждая прямая всегда может быть помещена в некоторую плоскость и при пересечении двух плоскостей образуется прямая, то в аналитической геометрии прямую в пространстве принято задавать как пересечение двух плоскостей. Итак, пусть
Систему (1) называют общими уравнениями прямой в пространстве. Так как через любую прямую в пространстве проходит множество плоскостей, то любую прямую можно задать ее общими уравнениями и не единственным образом. Недостатком задания прямой общими уравнениями является то, что по их виду ничего нельзя сказать о расположении прямой в пространстве. При решении задач удобнее использовать другие, более наглядные формы записи уравнений прямой – параметрические или канонические уравнения. Получим параметрические и канонические уравнения прямой в пространстве, решив следующую задачу. ЗАДАЧА 1. Записать уравнение прямой в пространстве, проходящей через точку Также, как и для прямой на плоскости, вектор, параллельный прямой в пространстве, называют направляющим вектором этой прямой.
Рассмотрим векторы Следовательно, существует такое число
или, в координатной форме,
Уравнение (2*) и систему уравнений (2) называют параметрическими уравнениями прямой в пространстве (в векторной и координатной форме соответственно). Если в задаче 1 вектор
и заменить систему (2) одним равенством вида:
где Уравнения (3) называют каноническими уравнениями прямой в пространстве.
Действительно, пусть прямая проходит через две точки
является ее направляющим вектором, и канонические уравнения этой прямой будут иметь вид
Уравнения (4) называют уравнениями прямой, проходящей через две заданные точки
|

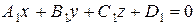 и
и 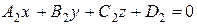 – уравнения любых двух различных плоскостей, содержащих прямую
– уравнения любых двух различных плоскостей, содержащих прямую 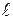 . Тогда координаты любой точки прямой
. Тогда координаты любой точки прямой 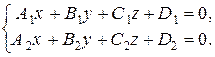 (1)
(1)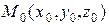 , параллельно вектору
, параллельно вектору 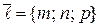 .
.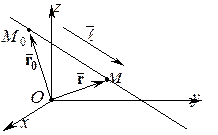 Пусть
Пусть 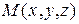 – текущая точка прямой. Обозначим через
– текущая точка прямой. Обозначим через 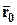 и
и 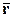 – радиус-векторы точек
– радиус-векторы точек 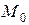 и
и 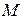 .
.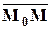
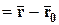 и
и 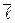 . По условию задачи они параллельны.
. По условию задачи они параллельны.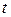 (
(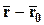
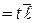 ,
,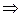
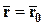
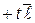 , (2*)
, (2*)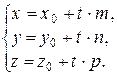 (2)
(2)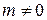 ,
, 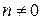 и
и 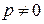 ), то из уравнений системы (2) можно выразить параметр
), то из уравнений системы (2) можно выразить параметр 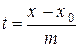 ,
, 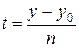 ,
, 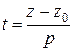
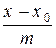
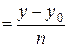
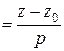 . (3)
. (3)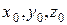 – координаты некоторой точки на прямой;
– координаты некоторой точки на прямой; 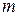 ,
, 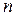 ,
, 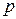 – координаты направляющего вектора прямой.
– координаты направляющего вектора прямой.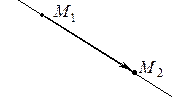 Частным случаем канонических уравнений являются уравнения прямой, проходящей через две заданные точки.
Частным случаем канонических уравнений являются уравнения прямой, проходящей через две заданные точки.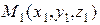 и
и 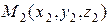 . Тогда вектор
. Тогда вектор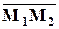
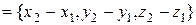
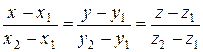 . (4)
. (4)


