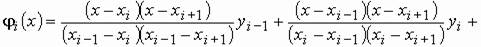Метод Симпсона
Многие инженерные задачи, задачи физики, геометрии и многих других областей человеческой деятельности приводят к необходимости вычислять определённый интеграл.
Суть приёма заключается в приближении подынтегральной функции на отрезке Разобьем отрезок интегрирования [a,b] на четное число n равных частей с шагом h. На каждом отрезке Коэффициенты этих квадратных трехчленов могут быть найдены из условий равенства многочлена в точках xi соответствующим табличным данным yi. В качестве j i(x) можно принять интерполяционный многочлен Лагранжа второй степени, проходящий через точки Mi-1(xi-1,yi-1), Mi(xi,yi), Mi+1(xi+1, yi+1):
Элементарная площадь si может быть вычислена с помощью определенного интеграла. Учитывая равенства xi+1 - xi = xi - xi-1 = h, получаем
Проведя такие вычисления для каждого элементарного отрезка [xi-1, xi+1], просуммируем полученные выражения:
Данное выражение для S принимается в качестве значения определенного интеграла:
Полученное соотношение называется формулой Симпсона.
|


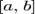 интерполяционным многочленом второй степени
интерполяционным многочленом второй степени  , то есть приближение графика функции на отрезке параболой. Метод Симпсона имеет порядок погрешности и алгебраический порядок точности. Метод Симпсона относится к приёмам численного интегрирования. Получила название в честь британского математика Томаса Симпсона (1710—1761)
, то есть приближение графика функции на отрезке параболой. Метод Симпсона имеет порядок погрешности и алгебраический порядок точности. Метод Симпсона относится к приёмам численного интегрирования. Получила название в честь британского математика Томаса Симпсона (1710—1761) подынтегральную функцию f(x) заменим интерполяционным многочленом второй степени:
подынтегральную функцию f(x) заменим интерполяционным многочленом второй степени: