Паралельний алгоритм Флойда-Уоршелла
При · головний процес відсилає k-й рядок та k-й стовпчик решті процесам
· далі головний процес відправляє всім процесам по n/numprocs рядків
· потім кожен процес обчислює свої рядки (включаючи 1-й) і відсилає їх на головний (у нашому випадку 0).
· головний процес збираю матрицю:
далі 3. Передача масиву з головного процесу на інші #include <stdio.h> #include "mpi.h" int main(int argc, char *argv[]) { int my_rank; int numprocs; int n,i; int a[100]; int temp[100]; int local_n; MPI_Init(&argc, &argv); MPI_Comm_rank(MPI_COMM_WORLD, &my_rank); MPI_Comm_size(MPI_COMM_WORLD, &numprocs); if (my_rank == 0) { printf("Input n:"); fflush(stdout); scanf("%d",&n); for (i=0; i<n; i++){ printf("Input a[%d]",i); fflush(stdout); scanf("%d",&a[i]); } } MPI_Bcast(&n,1,MPI_INT,0,MPI_COMM_WORLD); local_n=n/numprocs; MPI_Scatter(a,local_n,MPI_INT,temp,local_n,MPI_INT,0,MPI_COMM_WORLD); for (i=0; i<local_n; i++){ printf("%d",temp[i]); } printf("\n"); MPI_Finalize(); return 0; } 4. Передача масиву з усіх процесів на головний #include <stdio.h> #include "mpi.h" int main(int argc, char *argv[]) { int my_rank; int numprocs; int n,i; int a[100]; int temp[100]; int local_n; MPI_Init(&argc, &argv); MPI_Comm_rank(MPI_COMM_WORLD, &my_rank); MPI_Comm_size(MPI_COMM_WORLD, &numprocs); if (my_rank == 0) { printf("Input n:"); fflush(stdout); scanf("%d",&n); } MPI_Bcast(&n,1,MPI_INT,0,MPI_COMM_WORLD); local_n=n/numprocs; for (i=my_rank; i<n; i+=numprocs){ printf("Input a[%d]",i); fflush(stdout); scanf("%d",&a[i]); } MPI_Gather(a,local_n,MPI_INT,temp,local_n,MPI_INT,0,MPI_COMM_WORLD); if (my_rank==0){ for (i=0; i<n; i++){ printf("%d",temp[i]); } } MPI_Finalize(); return 0; } ІІ. Практична частина Інструкції до виконання 1. Застосовуючи технологію паралельного програмування МРІ, написати програму для знаходження найкоротших шляхів на заданому графі (варіанти згідно Додатку №3 лабораторної роботи №2) для будь-якої пари вершин графу, використовуючи паралельний алгоритм Флойда – Уоршелла. 2. Зробити висновки про швидкість виконання задачі при різній кількості комп’ютерів та процесів. Поточні контрольні питання: 1. За допомогою якої функції можна здійснити передачу даних від одного процесу всім іншим? 2. За допомогою якої функції можна здійснити передачу даних від всіх процесів до одного процесу? 3. Опишіть паралельний алгоритм Флойда-Уоршела. Рекомендована література: 1. Антонов А.С. Параллельное программирование с использованием технологии МРІ. 2. Воеводин В. В., Воеводин Вл. В. Параллельные вычисления. – СПб.: БХВ-Петербург, 2002. – 608. 3. Гергель В.П. Теория и практика параллельных вычислений/Гергель В. П. – М.: ИНТУИР.РУ Интернет-Университет Информационных технологий, 2007. 4. Гергель В. П., Фурсов В.А. Лекции по параллельным вычислениям: учебное пособие – Самара: Изд-во Самар. гос.аерокосм. ун-та, 2009. – 164с. 5. Корнеев В. Д. Параллельное программирование в МРІ. – 2-е изд., испр. – Новосисбирск: Изд-во ИВМиМГ СО РАН 2002. – 215с. Лабораторна робота №6 Мета: ознайомитися з паралельними алгоритмами матрично-векторного множення. Професійна спрямованість: через навчально-пізнавальну діяльність впливає на весь процес формування професійних цінностей і переконань. І. Теоретичні відомості 1. Послідовне множення матриці на вектор
Приклад
Розв’язання
Відповідь. 2. Алгоритм паралельного множення матриці на вектор 1) Визначаємо кількість процесів. 2) На головному процесі розділяємо матрицю А на смужки по рядках та розділяємо їх між процесами.
3) З головного процесу надсилаємо на кожен процес вектор В 4) На кожному процесі виконуємо множення відповідного рядка на вектор:
5) Результат множення з кожного процесу надсилається на головний процес і на ньому виконується збір результуючої матриці. 6) Приклад
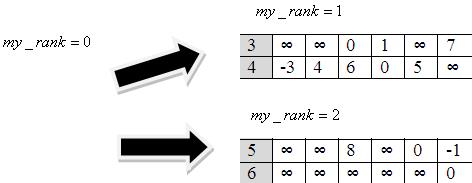
Алгоритм розв’язання: 1) Нехай ми маємо 3 процеси. 2) Розділяємо матрицю на смужки і надсилаємо: на процесі з рангом 0 (головний) залишиться смужка 3) З головного процесу надсилаємо на кожен процес вектор В 4) На кожному процесі виконуємо множення відповідного рядка на вектор: на процесі з рангом 0:
на процесі з рангом 1:
на процесі з рангом 2:
5) Результат множення з кожного процесу надсилається на головний процес і на ньому виконується збір результуючої матриці.
3. Послідовне множення матриці на матрицю
Приклад
Розв’язання
Відповідь. 4. Алгоритм паралельного множення матриці на матрицю 1) Визначаємо кількість процесів. 2) На головному процесі розділяємо матрицю А на смужки по рядках та розділяємо їх між процесами.
3) К дорівнює кількості стовпців у матриці В. 4) З головного процесу надсилаємо на кожен процес і-й стовпець матриці В 5) На кожному процесі виконуємо множення відповідного рядка на i-й стовпець матриці В
6) Результат множення з кожного процесу надсилається на головний процес і на ньому виконується збір відповідного стовпця результуючої матриці.
7) i збільшуємо на 1 і починаємо з 4) поки і<=k. Приклад
Алгоритм розв’язання: 1) Нехай ми маємо 3 процеси. 2) Розділяємо матрицю на смужки і надсилаємо: на процесі з рангом 0 (головний) залишиться смужка 3) 4) З головного процесу надсилаємо на кожен процес ( 5) На кожному процесі виконуємо множення відповідного рядка на і-й стовпець матриці В: на процесі з рангом 0:
на процесі з рангом 1:
на процесі з рангом 2:
6) Результат множення з кожного процесу надсилається на головний процес і на ньому виконується збір відповідного стовпця результуючої матриці.
7) i збільшуємо на 1 ( 8) З головного процесу надсилаємо на кожен процес ( 9) На кожному процесі виконуємо множення відповідного рядка на і-й стовпець матриці В: на процесі з рангом 0:
на процесі з рангом 1:
на процесі з рангом 2:
10) Результат множення з кожного процесу надсилається на головний процес і на ньому виконується збір відповідного стовпця результуючої матриці.
11) В результаті на головному процесі ми матимемо матрицю:
ІІ. Практична частина Інструкції до виконання 1. Виконати множення матриці на вектор. 2. Написати програму для множення матриці на вектор, використовуючи технологію паралельного програмування MPI. 3. Виконати множення матриці на матрицю. 4. Написати програму для множення матриці на матрицю, використовуючи технологію паралельного програмування MPI. Для 1-го та 2-го завдання варіанти згідно додатка №1, для 3-го та 4-го завдання варіанти згідно додатка №2. Поточні контрольні питання: 1. Опишіть алгоритм послідовного множення матриці на вектор. 2. Опишіть алгоритм паралельного множення матриці на вектор. 3. Опишіть алгоритм послідовного множення матриці на матрицю. 4. Опишіть алгоритм паралельного множення матриці на матрицю. Рекомендована література: 1. Антонов А.С. Параллельное программирование с использованием технологии МРІ. 2. Воеводин В. В., Воеводин Вл. В. Параллельные вычисления. – СПб.: БХВ-Петербург, 2002. – 608. 3. Гергель В.П. Теория и практика параллельных вычислений/Гергель В. П. – М.: ИНТУИР.РУ Интернет-Университет Информационных технологий, 2007. 4. Гергель В. П., Фурсов В.А. Лекции по параллельным вычислениям: учебное пособие – Самара: Изд-во Самар. гос.аерокосм. ун-та, 2009. – 164с. 5. Корнеев В. Д. Параллельное программирование в МРІ. – 2-е изд., испр. – Новосисбирск: Изд-во ИВМиМГ СО РАН 2002. – 215с. Додаток №1 1. Варіант
2. Варіант
4. Варіант
5. Варіант
6. Варіант
7. Варіант
8. Варіант
9. Варіант
10. Варіант
13. Варіант
14. Варіант
15. Варіант
16. Варіант
17. Варіант
18. Варіант
20. Варіант
22. Варіант
23. Варіант
Додаток №2 1. Варіант
4. Варіант
7. Варіант
9. Варіант
10. Варіант
15. Варіант
16. Варіант
17. Варіант
20. Варіант
22. Варіант
|




 ,
, 



 і т. д.
і т. д. .
. ,
, 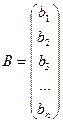

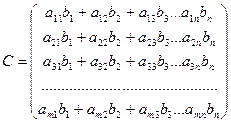 .
. .
. .
.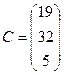



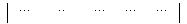


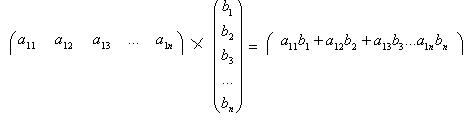 .
. ; на процес з рангом 1 відправиться смужка
; на процес з рангом 1 відправиться смужка  , тоді на процес з рангом 2 --
, тоді на процес з рангом 2 --  .
.



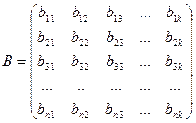


 .
. .
.



 .
.
 .
.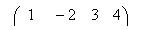 ; на процес з рангом 1 відправиться смужка
; на процес з рангом 1 відправиться смужка  , тоді на процес з рангом 2 --
, тоді на процес з рангом 2 --  .
. .
. ) і-й стовпець матриці В
) і-й стовпець матриці В 



 .
. ) і починаємо з 4).
) і починаємо з 4). ) і-й стовпець матриці В
) і-й стовпець матриці В 



 .
. .
.
 3. Варіант
3. Варіант





 11. Варіант
11. Варіант 12. Варіант
12. Варіант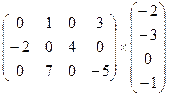





 19. Варіант
19. Варіант
 21. Варіант
21. Варіант

 24. Варіант
24. Варіант
 2. Варіант
2. Варіант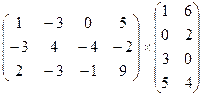 3. Варіант
3. Варіант
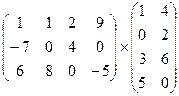 5. Варіант
5. Варіант 6. Варіант
6. Варіант
 8. Варіант
8. Варіант
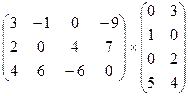
 11. Варіант
11. Варіант 12. Варіант
12. Варіант 13. Варіант
13. Варіант 14. Варіант
14. Варіант


 18. Варіант
18. Варіант 19. Варіант
19. Варіант
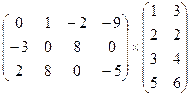 21. Варіант
21. Варіант
 23. Варіант
23. Варіант 24. Варіант
24. Варіант



