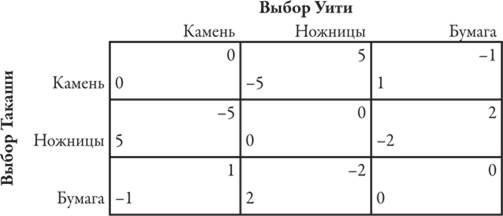
Анализ примера. Поскольку с каждой очередной ступенькой победитель продвигается вперед, а проигравший отстает, это игра с нулевой суммой

 

Поскольку с каждой очередной ступенькой победитель продвигается вперед, а проигравший отстает, это игра с нулевой суммой. Проанализировав все возможные пары ходов, получим матрицу игры. Выигрыши в этой таблице измеряются числом ступенек.

 

 

Как найти равновесное сочетание выбрасывания «бумаги», «ножниц» и «камня»? Мы уже рассказали о таких простых методах, как числовые расчеты и построение графика, которые применимы, когда у каждой стороны только одна альтернатива: удар справа и удар слева. Но в игре джанкен на ступеньках – три варианта выбора.

Прежде всего необходимо выяснить, какие стратегии войдут в состав равновесной смешанной стратегии. В данном случае важны все три варианта. Для того чтобы убедиться в этом, представьте себе, что Уити никогда не будет выбрасывать камень. В таком случае Такаши не станет играть бумагой; тогда Уити не будет выбрасывать ножницы. Если продолжить эту цепочку рассуждений, получится, что Такаши не будет использовать камень при условии, что Уити не использует бумагу. Если Уити никогда не будет выбрасывать камень, это сведет на нет все его стратегии, а значит, такое предположение было бы ложным. Аналогичные доводы подтверждают тот факт, что оставшиеся две стратегии тоже необходимо включить в смешанную стратегию Уити (и Такаши).

Теперь мы знаем, что в равновесной смешанной стратегии должны присутствовать все три стратегии. Остается выяснить, когда именно они будут использоваться. Игроки заинтересованы в получении максимального выигрыша, а не в смешивании стратегий ради самого смешивания. Уити готов использовать камень, ножницы и бумагу методом случайного выбора только при условии, что все три стратегии в равной степени привлекательны. (Если бы камень обеспечивал Уити более высокий выигрыш, чем ножницы или бумага, то ему следовало бы играть только камнем, но такая стратегия не была бы равновесной.) Таким образом, особый случай, когда все три стратегии обеспечивают Уити один и тот же ожидаемый выигрыш, определяет структуру равновесной смешанной стратегии Такаши.

Предположим, Такаши использует следующий принцип смешивания:

 

p = вероятность того, что Такаши выбросит бумагу;

q = вероятность того, что Такаши выбросит ножницы;

1 – (p + q) = вероятность того, что Такаши выбросит камень.

 

В таком случае, если Уити сыграет камнем, он будет отставать на пять ступенек, если Такаши сыграет бумагой (р), и выиграет одну ступеньку, если Такаши сыграет ножницами (q), а чистый выигрыш составит –5 p + q. Точно так же Уити получит следующий выигрыш за счет каждой из своих стратегий:

 

Камень: –5 p + 1 q + 0(1 – (p + q)) = –5 p + q.

Ножницы: 2 p + 0 q – 1(1 – (p + q)) = 3 p + q – 1.

Бумага: 0 p – 2 q + 5(1 – (p + q)) = –5 p – 7 q + 5.

 

Эти три варианта могут быть в равной степени привлекательными для Уити только при выполнении следующего условия:

 

– 5 p + q = 3 p + q – 1 = –5 p – 7 q + 5.

 

Решив эти уравнения, получим: p = 1∕8, q = 5∕8 и (1 – p – q) = 2∕8.

Это определяет структуру равновесной смешанной стратегии Такаши. Поскольку эта игра симметрична, Уити будет использовать свои стратегии по методу случайного выбора с такой же вероятностью.

Обратите внимание на то, что, если и Уити, и Такаши используют свое равновесное сочетание стратегий, их ожидаемый выигрыш за счет каждой стратегии будет равен нулю. К такому исходу игры приводят не все смешанные стратегии, однако в симметричных играх с нулевой суммой возможен только такой результат. Нет причин, почему Уити должен находиться в более выгодном положении, чем Такаши, и наоборот.

В главе 14 рассматривается еще один учебный пример, посвященный теме выбора и случая, – «Как обмануть всех: игровые автоматы Лас-Вегаса».