Также односторонние пределы  ,
,  говорят нам о том, что гипербола не ограничена сверху и не ограничена снизу.
говорят нам о том, что гипербола не ограничена сверху и не ограничена снизу.
Исследуем функцию на бесконечности:  , то есть, если мы начнем уходить по оси
, то есть, если мы начнем уходить по оси  влево (или вправо) на бесконечность, то «игреки» стройным шагом будут бесконечно близко приближаться к нулю, и, соответственно, ветви гиперболы бесконечно близко приближаться к оси
влево (или вправо) на бесконечность, то «игреки» стройным шагом будут бесконечно близко приближаться к нулю, и, соответственно, ветви гиперболы бесконечно близко приближаться к оси  .
.
Таким образом, ось  является горизонтальной асимптотой для графика функции
является горизонтальной асимптотой для графика функции 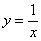 , если «икс» стремится к плюс или минус бесконечности.
, если «икс» стремится к плюс или минус бесконечности.
Функция 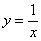 является нечётной, а, значит, гипербола симметрична относительно начала координат. Данный факт очевиден из чертежа, кроме того, легко проверяется аналитически:
является нечётной, а, значит, гипербола симметрична относительно начала координат. Данный факт очевиден из чертежа, кроме того, легко проверяется аналитически:  .
.
График функции вида (
( ) представляют собой две ветви гиперболы.
) представляют собой две ветви гиперболы.
Если , то гипербола расположена в первой и третьей координатных четвертях (см. рисунок выше).
, то гипербола расположена в первой и третьей координатных четвертях (см. рисунок выше).
Если , то гипербола расположена во второй и четвертой координатных четвертях.
, то гипербола расположена во второй и четвертой координатных четвертях.
Указанную закономерность места жительства гиперболы нетрудно проанализировать с точки зрения геометрических преобразований графиков.
Пример 3
Построить правую ветвь гиперболы 
Используем поточечный метод построения, при этом, значения  выгодно подбирать так, чтобы делилось нацело:
выгодно подбирать так, чтобы делилось нацело:

Выполним чертеж:

Не составит труда построить и левую ветвь гиперболы, здесь как раз поможет нечетность функции. Грубо говоря, в таблице поточечного построения мысленно добавляем к каждому числу минус, ставим соответствующие точки и прочерчиваем вторую ветвь.

 ,
,  говорят нам о том, что гипербола не ограничена сверху и не ограничена снизу.
говорят нам о том, что гипербола не ограничена сверху и не ограничена снизу. , то есть, если мы начнем уходить по оси
, то есть, если мы начнем уходить по оси  влево (или вправо) на бесконечность, то «игреки» стройным шагом будут бесконечно близко приближаться к нулю, и, соответственно, ветви гиперболы бесконечно близко приближаться к оси
влево (или вправо) на бесконечность, то «игреки» стройным шагом будут бесконечно близко приближаться к нулю, и, соответственно, ветви гиперболы бесконечно близко приближаться к оси 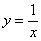 , если «икс» стремится к плюс или минус бесконечности.
, если «икс» стремится к плюс или минус бесконечности. .
. (
( ) представляют собой две ветви гиперболы.
) представляют собой две ветви гиперболы. , то гипербола расположена в первой и третьей координатных четвертях (см. рисунок выше).
, то гипербола расположена в первой и третьей координатных четвертях (см. рисунок выше). , то гипербола расположена во второй и четвертой координатных четвертях.
, то гипербола расположена во второй и четвертой координатных четвертях.
 выгодно подбирать так, чтобы делилось нацело:
выгодно подбирать так, чтобы делилось нацело:




