Трапеция. Средняя линия трапеции. Признаки и свойства равнобедренной трапеции.
Замечание: Сумма двух углов трапеции, прилежащих к ее боковой стороне, равна 180°, поскольку они являются внутренними односторонними углами при параллельных прямых (основаниях трапеции) и секущей.
Замечание: Высота трапеции равна расстоянию между ее основаниями. Трапеция называется прямоугольной (сокращенно – п/у трапеция), если один из ее углов прямой (рисунок 18).
Трапеция называется равнобедренной (равнобокой, равнобочной), если равны ее боковые стороны (сокращенно – р/б трапеция) (рисунок 19). Средней линией трапеции называется отрезок, соединяющий середины ее боковых сторон (на рисунке 20 MN – средняя линия трапеции ABCD).
Теорема о средней линии трапеции: Средняя линия трапеции параллельна ее основаниям и равна их полусумме.
ABCD – трапеция; BC ïê AD; M – середина AB;
Доказать: MN ïê AD;
Доказательство: 1. Проведем прямую BN: BN Ç AD = Q. 2. D BCN =D QDN по стороне и прилежащим к ней углам (CN = ND, Ð CNB =Ð DNQ как вертикальные, Ð BCN =Ð QDN как внутр. н/л при BC ïê AD и секущей CD), Þ BC = QD, BN = QN. 3. AM = MB, BN = QN, Þ MN – ср. л. D ABQ, Þ по теореме о средней линии треугольника MN ïê AQ, Свойство равнобедренной трапеции: В равнобедренной трапеции равны углы при основаниях и диагонали (рисунок 21).
ABCD – р/б трапеция;
Доказать: Ð A =Ð D; Ð B =Ð C; AC = BD. Доказательство: 1. Проведем CP ïê AB: P Î AD. 2. CP ïê AB, BC ïê AP; Þ ABCP - п/г по определению; Þ AB = CP. 3. CD = AB = CP, Þ CD = CP; Þ D PCD - р/б; Þ по свойству углов при основании равнобедренного треугольника Ð CPD =Ð D. 4. Ð CPD и Ð A – соответственные при CP ïê AB и секущей AD; Þ Ð CPD =Ð A. 5. Из пп. 3, 4 Ð A =Ð CPD =Ð D; Þ Ð A =Ð D; Ð B =180°-Ð A =180°-Ð D =Ð C. Таким образом, равенство углов доказано. 6. D ABD =D DCA по двум сторонам и углу между ними (AD – общая; AB = CD, Ð A =Ð D из п. 3); Þ AC = BD. # Свойство высоты равнобедренной трапеции: Высота равнобедренной трапеции, проведенная к ее большему основанию, разбивает это основание на два отрезка, меньший из которых равен полуразности оснований, а больший – полусумме (рисунок 22).
ABCD – р/б трапеция; BC ïê AD; BC < AD;
Доказать:
Доказательство: 1. Проведем высоту CF. 2. D ABH =D DCF по гипотенузе и острому углу (AB = CD по определению р/б трапеции; Ð A =Ð D по свойству р/б трапеции); Þ AH = FD. 3. HBCF – п/г по определению (BC ïê HF по определению трапеции; BH ïê CF, т.к. BH ^ AD ^ CF); Þ HF = BC. 4. AD = AH + HF + FD = AH + BC + AH =2 AH + BC; Þ 5.
Определить, что трапеция является равнобедренной, позволяют следующие признаки: · Признак равнобедренной трапеции по углам: Если в трапеции углы при основании равны, то она является равнобедренной (рисунок 23). Дано: ABCD – трапеция; BC ïê AD;
Доказать: ABCD - р/б.
1. Проведем BT ïê CD: T Î AD. 2. Ð BTA =Ð D как соответственные при BT ïê CD и секущей AD; Þ Ð BTA =Ð D =Ð A; Þ D ABT - р/б по признаку р/б D‑ка; Þ AB = BT. 3. BC ïê AD, BT ïê CD; Þ BTDC - п/г по определению; Þ BT = CD по свойству п/г. 4. AB = BT = CD; Þ AB = CD, Þ ABCD - р/б по определению. #
· Признак равнобедренной трапеции по диагоналям: Если в трапеции диагонали равны, то она является равнобедренной (рисунок 24). Дано: ABCD – трапеция; BC ïê AD;
Доказать: ABCD - р/б.
1. Проведем CV ïê BD: V Î AD. 2. BC ïê AD, CV ïê BD, Þ BCVD – п/г по определению, Þ CV = BD по свойству п/г. 3. CV = BD = AC; Þ CV = AC, Þ D ACV - р/б по определению; Þ Ð CAV =Ð CVA по свойству р/б D-ка. 4. Ð CVA =Ð BDA как соответственные при CV ïê BD и секущей AV. 5. Ð CAV =Ð CVA =Ð BDA; Þ Ð CAV =Ð BDA. 6. D ABD =D DCA по двум сторонам и углу между ними (AD – общая, AC = BD по условию, Ð CAD =Ð BDA); Þ AB = CD; Þ ABCD - р/б по определению. # Замечание: Дополнительные построения, изображенные на рисунках 21-24, заслуживают пристального внимания, поскольку они часто используются в задачах о трапеции («сдвиг» боковых сторон, «раздвижение» диагоналей, проведение второй высоты в равнобедренной трапеции).
|

 Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие – непараллельны. При этом параллельные стороны называются основаниями трапеции, а непараллельные – боковыми сторонами.
Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие – непараллельны. При этом параллельные стороны называются основаниями трапеции, а непараллельные – боковыми сторонами. Высотой трапеции называется перпендикуляр, опущенный из ее вершины к прямой, содержащей противолежащее основание (на рисунке 17 AD и BC – основания; AB и CD – боковые стороны, BH – высота трапеции ABCD).
Высотой трапеции называется перпендикуляр, опущенный из ее вершины к прямой, содержащей противолежащее основание (на рисунке 17 AD и BC – основания; AB и CD – боковые стороны, BH – высота трапеции ABCD). Замечание: В прямоугольной трапеции два прямых угла, а одна из боковых сторон является высотой.
Замечание: В прямоугольной трапеции два прямых угла, а одна из боковых сторон является высотой. Дано:
Дано: N – середина CD.
N – середина CD. .
.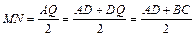 . #
. # Дано:
Дано: BC ïê AD.
BC ïê AD. Дано:
Дано: BH – высота.
BH – высота. ;
; .
. . #
. # Доказательство:
Доказательство: Доказательство:
Доказательство:


