Прямоугольник, ромб, квадрат.
Прямоугольником называется параллелограмм, все углы которого прямые (рисунок 25). Замечание 1: Если в параллелограмме есть хотя бы один прямой угол, то все остальные его углы тоже прямые, а значит, параллелограмм с прямым углом является прямоугольником. Замечание 2: Если в четырехугольнике есть три прямых угла, то четвертый его угол также будет прямым, и стороны такого четырехугольника окажутся попарно параллельными. Поэтому четырехугольник, три угла которого прямые, также является прямоугольником. Замечание 3: Поскольку прямоугольник является параллелограммом, он обладает всеми свойствами параллелограмма, т.е. противоположные стороны прямоугольника равны, а диагонали точкой пересечения делятся пополам. Прямоугольник обладает также особым свойством: Свойство диагоналей прямоугольника: Диагонали прямоугольника равны (рисунок 26). Дано:
Доказать: AC = BD.
1. D BAD =D CDA по двум катетам (AD – общий, AB = CD по свойству п/г), Þ BD = AC. #
Справедлива и обратная теорема:
Дано:
Доказать: ABCD - прямоугольник. Доказательство: 1. D BAD =D CDA по трем сторонам (AD – общая, AB = CD по свойству п/г, AC = BD по условию), Ð A =Ð D. 2. Ð A +Ð D =180° как внутр. о/с при AB ïê CD и секущей AD; Þ Ð A =Ð D =180°:2=90°. 3. По свойству п/г Ð C =Ð A =90°, Ð B =Ð D =90°, Þ ABCD – прямоугольник по определению. # Ромбом называется параллелограмм, все стороны которого равны (рисунок 28). Замечание 1: Если у четырехугольника все стороны равны, то он является параллелограммом по признаку, а значит, является параллелограммом, все стороны которого равны. Таким образом, ромбом можно назвать четырехугольник, все стороны которого равны. Замечание 2: Поскольку ромб является параллелограммом, он обладает всеми свойствами параллелограмма. В частности, у ромба попарно равны противоположные углы, а диагонали точкой пересечения делятся пополам. Помимо свойств параллелограмма, ромб обладает также особым свойством: Свойство ромба: Диагонали ромба взаимно перпендикулярны и являются биссектрисами его углов (рисунок 28).
Доказать: AC ^ BD; AC – биссектриса углов A и C; BD – биссектриса углов B и D. Доказательство: 1. Обозначим O = AC Ç BD. 2. По определению ромба AB = AD, Þ D ABD – р/б. 3. По свойству п/г BO = OD, Þ AO – медиана D ABD, Þ по свойству медианы р/б D-ка AO – его биссектриса и высота. А значит, AC ^ BD, и AC – биссектриса угла A. 4. Аналогично доказывается, что AC – биссектриса угла C, а BD – биссектриса углов B и D. # Замечание: Перпендикулярность диагоналей ромба используется при его изображении: рисуется два взаимно перпендикулярных отрезка, которые точкой пересечения делятся пополам, и последовательно соединяются четыре их конца (рисунок 29). Определить, что параллелограмм является ромбом, позволяют следующие признаки: · Признак ромба по взаимно перпендикулярным диагоналям: Если диагонали параллелограмма взаимно перпендикулярны, то этот параллелограмм – ромб (рисунок 29).
ABCD – п/г;
Доказать: ABCD – ромб. Доказательство: 1. Обозначим O = AC Ç BD. 2. Поскольку ABCD – п/г, AO = OC по свойству диагоналей п/г. 3. BO – высота и медиана D ABC, Þ D ABC - р/б по признаку, Þ AB = BC. 4. По свойству противоположных сторон п/г AB = CD, BC = AD. Таким образом, CD = AB = BC = AD, то есть все стороны п/г ABCD равны, Þ ABCD – ромб. # · Признак ромба по диагонали: Если диагональ параллелограмма является биссектрисой его угла, то этот параллелограмм – ромб (рисунок 30).
ABCD – п/г;
Доказать: ABCD – ромб. Доказательство: 1. Обозначим O = AC Ç BD. 2. Поскольку ABCD – п/г, AO = OC по свойству диагоналей п/г. 3. AO – биссектриса и медиана D ABD, Þ D ABD - р/б по признаку, Þ AB = AD. 4. По свойству противоположных сторон п/г AB = CD, BC = AD. Таким образом, CD = AB = AD = BC, то есть все стороны п/г ABCD равны, Þ ABCD – ромб. #
Квадратом называется прямоугольник, все стороны которого равны (рисунок 31). Замечание: Квадрат является и параллелограммом, и прямоугольником, и ромбом, поэтому сочетает в себе все их свойства. В частности, диагонали квадрата равны, точкой пересечения делятся пополам, взаимно перпендикулярны и являются биссектрисами его углов (рисунок 31).
|


 ABCD – прямоугольник.
ABCD – прямоугольник. Доказательство:
Доказательство: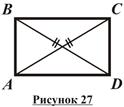 Признак прямоугольника: Если диагонали параллелограмма равны, то он является прямоугольником (рисунок 27).
Признак прямоугольника: Если диагонали параллелограмма равны, то он является прямоугольником (рисунок 27). Дано:
Дано: ABCD – ромб.
ABCD – ромб. Дано:
Дано: AC ^ BD.
AC ^ BD.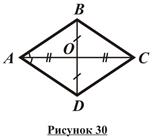 Дано:
Дано:



