Параллелограмм, его свойства и признаки.
Замечание: Сумма двух соседних углов параллелограмма равна 180°, поскольку они являются внутренними односторонними углами при параллельных прямых и секущей. Высотой параллелограмма называется перпендикуляр, опущенный из его вершины к прямой, содержащей одну из противолежащих сторон (на рисунке 6 CF и CH – высоты параллелограмма ABCD). Замечание: Высота параллелограмма равна расстоянию между его противоположными сторонами (на рисунке 6 Параллелограмм обладает следующими свойствами: · Свойство противоположных сторон и углов параллелограмма: В параллелограмме противоположные стороны попарно равны, и противоположные углы попарно равны (рисунок 7). Дано:
Доказать: AB = CD, BC = AD, Ð A =Ð C, Ð B =Ð D.
Доказательство: 1. Проведем диагональ BD. 2. Ð ABD =Ð CDB как внутренние накрест лежащие (сокращенно – внутр. н/л) углы при параллельных прямых AB, CD и секущей BD. 3. Ð ADB =Ð CBD как внутр. н/л углы при AD ïê BC и секущей BD. 4. D ABD =D CDB по стороне и двум прилежащим к ней углам (BD – общая сторона, Ð ABD =Ð CDB, Ð ADB =Ð CBD); Þ AB = CD, AD = CB, Ð A =Ð C. Кроме того, Ð B =Ð ABD +Ð CBD =Ð CDB +Ð ADB =Ð D. #
· Свойство диагоналей параллелограмма: Диагонали параллелограмма точкой пересечения делятся пополам (рисунок 8). Дано: ABCD – п / г;
Доказать: AO = OC, BO = OD.
Доказательство: 1. Ð ADB =Ð CBD как внутр. н/л углы при AD ïê BC и секущей BD; 2. Ð CAD =Ð ACB как внутр. н/л углы при AD ïê BC и секущей AC; 3. AD = BC по свойству противоположных сторон и углов параллелограмма. 4. D COB =D AOD по стороне и двум прилежащим к ней углам (BC = AD, Ð OCB =Ð OAD, Ð CBO =Ð ADO); Þ OB = OD, CO = AO. #
Оказывается, определить, что четырехугольник является параллелограммом, можно по следующим признакам параллелограмма: · Признак параллелограмма по двум сторонам: Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – параллелограмм (рисунок 9).
ABCD – четырехугольник;
Доказать: ABCD - п/г. Доказательство: 1. Проведем диагональ AC. 2. AB ïê CD; Þ Ð BAC =Ð DCA как внутр. н/л углы при AB ïê CD и секущей AC; 3. D ABC= D CDA по двум сторонам и углу между ними (AC – общая сторона, AB = CD по условию, Ð BAC =Ð DCA); Þ Ð BCA =Ð DAC; 4. Ð BCA и Ð DAC – внутр. н/л углы при прямых AD, BC и секущей AC; т.к. они равны, то AD ïê BC по признаку параллельности прямых. 5. AB ïê CD по условию; AD ïê BC по доказанному; Þ ABCD - п/г по определению. # · Признак параллелограмма по противоположным сторонам: Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм.
ABCD – четырехугольник;
Доказать: ABCD - п/г. Доказательство: 1. Проведем диагональ BD. 2. D ABD= D CDB по трем сторонам (BD – общая сторона, AB = CD и BC = AD по условию); Þ Ð BDA =Ð DBC; 3. Ð BDA и Ð DBC – внутр. н/л при прямых AD, BC и секущей BD; т.к. Ð BDA =Ð DBC, то AD ïê BC по признаку параллельности прямых. 4. AD = BC по условию; AD ïê BC по доказанному; Þ ABCD - п/г по признаку параллелограмма по двум сторонам. #
· Признак параллелограмма по углам: Если в четырехугольнике противоположные углы попарно равны, то этот четырехугольник – параллелограмм (рисунок 11).
ABCD – четырехугольник; Ð; Доказать: ABCD - п/г. Доказательство: 1. Обозначим ÐA =Ð C = a; Ð B= Ð D = b. 2. Поскольку ABCD – четырехугольник, сумма его внутренних углов равна 180°×(4-2)=360°. Тогда ÐA +Ð B +Ð C +Ð D = a + b + a + b =2×(a + b)=360°; Þ a + b =180°. 3. Ð A и Ð B – внутренние односторонние (сокращенно – внутр. о/с) углы при прямых AD, BC и секущей AB; поскольку Ð A +Ð B = a + b =180°, то по признаку параллельности прямых AD ïê BC. 4. Ð A и Ð D – внутр. о/с при прямых AB, CD и секущей AD; поскольку Ð A +Ð D = a + b =180°, то по признаку параллельности прямых AB ïê CD. 5. Из доказанного AD ïê BC, AB ïê CD; Þ ABCD - п/г по определению. #
· Признак параллелограмма по диагоналям: Если диагонали четырехугольника точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм (рисунок 12). Дано: ABCD – четырехугольник; AC Ç BD=O; AO=OC Доказать: ABCD - п/г.
Доказательство: 1. D AOB =D COD по двум сторонам и углу между ними (AO=OC; BO=OD, Ð AOB =Ð COD как вертикальные); Þ AB = CD, Ð BAO =Ð DCO. 2. Ð BAO и Ð DCO – внутр. н/л при прямых AB, CD и секущей AC; т.к. Ð BAO =Ð DCO, то AB ïê CD по признаку параллельности прямых. 3. AB = CD, AB ïê CD, Þ ABCD – п/г по признаку параллелограмма по двум сторонам. #
|

 Параллелограммом (сокращенно – п/г) называется четырехугольник, у которого противоположные стороны попарно параллельны (рисунок 6):
Параллелограммом (сокращенно – п/г) называется четырехугольник, у которого противоположные стороны попарно параллельны (рисунок 6): .
. ;
;  ).
). ABCD – п/г.
ABCD – п/г.
 AC Ç BD = O.
AC Ç BD = O.
 Дано:
Дано: AB = CD; AB ïê CD.
AB = CD; AB ïê CD.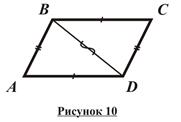 Дано:
Дано: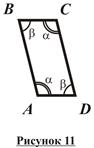 Дано:
Дано:



