Спрощені моделі врахування ризику у величині норми дисконту
У літературі характеризують ризик як діяльність щодо прий- Якщо спостерігається мінливість доходів, то чим більше коливаються (відхиляються) доходи, тим вищий ризик. Цю мінливість часто вимірюють за допомогою стандартного відхилення. Зв’язок між величиною очікуваного доходу R і ступенем ризику обчислюється, зокрема, за формулою
де Rj — безпечна ставка доходу; s p — стандартне відхилення заданої комбінації цінних паперів з ризиковими та безризиковими активами. Щоб виконувати математичні розрахунки рівня ризику, потрібно знати теорію ймовірностей, математичне моделювання та розуміти, як ризик портфеля цінних паперів і доходи поєднуються у своїй взаємозалежності. Розроблено також модель оцінювання капітальних активів (МОКА), тобто модель, що пов’язує прогнозований ризик зі сподіваними доходами від проекту. МОКА поділяє ризик на дві складові: диверсифікований та недиверсифікований. Ідеться про тісний зв’язок між доходами окремих власників цінних паперів і загальними доходами ринку цінних паперів. Ці доходи, узяті окремо для акцій або для всього ринку, складаються з доходів від капітальних вкладень та дивідендів. Науковці довели, що фондова біржа — високоефективний механізм, бо вона швидко поєднує всю наявну інформацію. Якщо це так, то мінливість ринку має загальний визначник для оцінювання рівня ризику (або мінливості) індивідуальних активів і цінних паперів. Цей рівень ризику визначається чутливістю доходів від акцій до ситуації на ринку. Рівняння, що спрощено відбиває залежність між дохідністю R та дохідністю ринку, має вигляд R = b Rm + a + e, (4.19) де b — коефіцієнт, що визначає міру чутливості або ризикованість акцій порівняно із загальною дохідністю ринку; Rm — дохідність ринку; a — деяка константа; e — значення помилки. У більш спрощеній моделі МОКА величини а та е прирівнюються до нуля. Зрозуміло, що МОКА дає змогу легко порівнювати ризикованість окремих акцій. Проте важливою передумовою є те, що дисперсія навколо лінії (4.19) не повинна бути великою. Якщо дисперсія велика, слід ураховувати додаткові елементи ризику, скористатися нелінійними моделями. Модель лінії надійності ринку (ЛНР) показує, що необхідна величина дохідності активів складається з безпечної ставки та премії за ризик. Якщо оцінювати ризик за допомогою коефіцієнта β, то формулу для визначення необхідної дохідності акцій (ставки доходу) можна подати так:
де Rj — безпечна ставка; Rm — середня дохідність ринку; b — бета, або недиверсифiковуваний ризик. Безумовною перевагою МОКА та ЛНР є простота. Це корисний інструмент для оцінювання цінних паперів, який дає змогу визначити необхідну ставку доходу (дисконтну ставку), а останню можна використати для знаходження теперішньої вартості цінних паперів. Замість того щоб теперішню вартість сподіваних доходів знаходити за формулою
доцільніше скористатися спрощеною залежністю
де FV n — майбутня вартість сподіваних доходів; п — кількість років. Зрештою, який би метод не застосовувався для врахування ризику — стандартне відхилення чи показник β, — обидва створюють підґрунтя для оцінювання активів. МОКА та ЛНР не такі вже й бездоганні, можливі й інші суттєві чинники, що впливають на визначення ставки дисконту. Те саме стосується й використання статистичних рядів за певний період часу, тобто це не найкращий спосіб визначення сподіваних доходів. 4.3.3. Імовірнісна модель Постановка задачі. Процес одержання доходу від функціонування об’єкта характеризується інтенсивністю (швидкістю) x (t). Тоді дохiд, одержуваний за досить малий інтервал часу (t, t + dt), буде x (t) dt. Вважатимемо відомою інтенсивність одержання доходу х (0) = Х на початку функціонування об’єкта (у момент часу t = 0). На подальшу динаміку цього показника впливають дві групи чинників. 1. Фізична зношуваність основних засобів. Припустимо, що залежно від віку основних засобів дохід зменшується лінійно: x (t) = X – bt. (4.22) Відомо, що об’єкт доцільно експлуатувати доти, поки дохід від нього не від’ємний. Тому в кінці терміну експлуатації (у рік Т) має бути x (Т) = 0. Звідси
2. Різного роду випадкові чинники, що зумовлюють ризик використання об’єкта. Якби їх впливу не було або він був неістотним, то за відомої норми дисконту дохід від функціонування об’єкта обчислювався б за формулою:
Вважатимемо відомими (виокремимо) три типи випадкових чинників, що впливають на дохідність об’єкта: випадкові «збої» у виробництві; різкі зміни економічного середовища («катастрофи»); випадкові коливання цін, податків та обсягів попиту. Щоб адекватно відобразити ці чинники в нормі дисконту R, потрібно виконати два варіанти розрахунку дохідності від роз- У першому, що використовує норму дисконту R, згадані випадкові чинники взагалі не беруться до уваги, а інтегральний дисконтований дохід оцінюється згідно з (4.24). У другому, що спирається на «безризикову» норму Rj, ці чинники включаються безпосередньо у відповідну модель випадкового процесу зміни інтенсивності доходу. Тоді значення норми дисконту R, яке враховує чинники ризику, доцільно зробити такими, щоб обидва варіанти розрахунків однаково оцінювали ефективність функціонування об’єкта. Розгляньмо докладніше моделювання доходу з урахуванням перелічених чинників ризику. Випадкові «збої» у виробництві. Нехай у момент t об’єкт характеризувався деякою інтенсивністю одержання доходу x (t). Тоді протягом наступного малого інтервалу часу dt або відбудеться «збій» у виробництві з імовірністю w dt, або об’єкт функціонуватиме «нормально» з імовірністю 1 – w dt. Якщо «збій» відбувся, то на його усунення потрібен деякий час t (вважатимемо цю величину малою, але не нескінченно малою), а також знадобляться додаткові витрати x, взагалі кажучи, випадкові. Вважатимемо, що після цього виробництво повертається до свого попереднього стану, тобто «збій» не зменшує часу функціо- «Катастрофи». Поряд з даним покупцем (власником об’єкта) той самий вид діяльності здійснюють інші підприємці. Може статися так, що хтось із них розробить новий ефективний спосіб (технологію) виробництва відповідної продукції, у зв’язку з чим ціна на продукцію різко впаде. Тоді подальше функціонування першого об’єкта вже не забезпечуватиме доходу, що для підприємця стане економічною катастрофою. Аналогічна ситуація можлива й тоді, коли істотно зміниться чинне податкове законодавство або політична ситуація в регіоні. Нехай імовірність такої «катастрофи» в інтервалі (t, t + dt) дорівнює kdt, де k — інтенсивність «катастроф», що не залежать від t. Оцінювати ймовірність таких ситуацій можливо лише експертно, з урахуванням результатів аналізу науково-технічного прогресу у відповідній виробничій галузі (підгалузі) і прогнозу економічної та політичної ситуації. Оскільки величини k і t — малі, «катастрофи» у період існування наслідків «збою» вважатимемо неможливими. Коливання цін податків та обсягів попиту. Протягом періоду функціонування об’єкта ціни на продукцію, яка виготовляється, сировину, матеріали, комплектувальні вироби, а також обсяги попиту та ставки податку можуть змінюватися. Під впливом цих чинників інтенсивність одержуваного доходу також випадково коливатиметься. Якщо припустимо, що в момент оцінювання об’єкта були правильно визначені розміри доходу, то коливання інтенсивності x (t), зумовлені групою розглянутих щойно чинників, матимуть нульове математичне сподівання, але характеризуватимуться певним розкидом (дисперсією). Природно сподіватися, що в малому інтервалі часу випадкові коливання x (t) мають малу дисперсію, а інтенсивність x (t) не залежить від розмірів таких коливань у попередні відрізки часу. З огляду на це можна припустити, що ці коливання описуються моделлю вінерівського випадкового процесу, тобто що інтенсивність доходу в близькі моменти часу t i t + dt задовольняє співвідношення x (t + dt) = x (t) +s d w(t), (4.25) де s — середньоквадратичне відхилення випадкових коливань інтенсивності доходу x (t) за одиницю часу (середній квадрат таких коливань за час dt дорівнюватиме за цих умов s2 dt; w(t) — звичайний вінерівський випадковий процес. Математичне сподівання доходу в разі урахування чинників ризику. Позначимо через V (x) значення математичного сподівання інтегрального дисконтованого доходу (за норми дисконту Rj) від експлуатації об’єкта до закінчення терміну його функціонування (випадкова величина). Нехай у початковий момент виробництво функціонувало «нормально», а інтенсивність одержуваного доходу була x. Очевидно, що V (0) = 0. Природно розглядати випадок, коли x > 0. Зауважимо, що для визначенні V (x) не має значення, який, власне, момент часу брати за початковий. Це дає змогу дисконтувати доходи до моменту t = 0. Розгляньмо малий інтервал часу (0, dt). Тут можливі три ситуації. 1. З імовірністю w dt станеться збій у виробництві. На усунення його наслідків знадобляться витрати (випадкова величина), дисконтована величина яких x. Виробництво нормалізується через випадковий проміжок часу t (випадкова величина), після чого об’єкт перейде до нормального стану, якому відповідає математичне сподівання інтегрального дисконтованого доходу V (x). У цьому разі різночасові доходи зводяться до часу повної ліквідації наслідків «збою». Якщо звести дохід до моменту t = 0, то величину V (x) слід помножити на відповідний дисконтуючий коефіцієнт За припущення, що час ліквідації «збою» випадковий і підлягає експоненціальному закону розподілу із середнім значенням q, математичне сподівання М дисконтуючого коефіцієнта можна подати у вигляді
Вважаючи, що додаткові витрати в процесі усунення наслідків збою відбуваються рівномірно, а їх величина за одиницю часу становить z, знайдемо математичне сподівання дисконтованих витрат, пов’язаних з одним «збоєм»:
2. Упродовж інтервалу (0, dt) часу з імовірністю kdt відбудеться економічна катастрофа. У такому разі виробництво зупиниться, а тому інтегральний дисконтований дохід від наступного функціонування об’єкта набуде нульового значення. 3. На інтервалі (0, dt) з імовірністю 1 – (w + k) dt об’єкт функціонуватиме «нормально». Тоді за час dt дохiд становитиме x (t) dt, після чого інтенсивність його одержання зміниться на величину bdt за рахунок фізичного старіння основних засобів, а також згідно з (4.25) — на s d w(t) під впливом випадкових коливань цін і (або) податків. Тому в момент часу dt об’єкт характеризуватиметься інтенсивністю доходу x – bdt + s d w(t). Цьому відповідає інтегральний дисконтований (до моменту 0, а не d (t)) дохід, що
Ураховуючи ймовірність кожної з розглянутих ситуацій і той стан, у якому перебуває об’єкт після них, можна записати вираз для математичного сподівання інтегрального дисконтованого доходу від функціонування об’єкта:
З урахуванням (4.25), (4.27) це рівняння з точністю до малих величин порядку, вищого за перший, можна замінити таким:
Припустимо, що функція V досить гладка, і за умови x > 0 її друга похідна V'' (x) існує і є неперервною. Тоді, розклавши останній співмножник у ряд Тейлора і врахувавши, що величина d w(t) має нульове значення математичного сподівання та дисперсію
Звідси маємо рівняння
Де d = Rj + k + (1 – q)w. (4.30)
|

 , (4.18)
, (4.18)
 (4.20)
(4.20) (4.21)
(4.21) або
або  (4.23)
(4.23) (4.24)
(4.24) .
. (4.26)
(4.26) (4.27)
(4.27)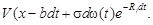

 (4.28)
(4.28) , знайдемо:
, знайдемо:
 (4.29)
(4.29)


