Прогнозування обсягів податкових надходжень з урахуванням ризику
Спинімося на деяких питаннях прогнозування обсягів надходжень податків, які ґрунтуються на даних, що характеризують тенденції зміни загальноекономічних показників розвитку країни, галузей народного господарства, конкретного регіону, та методичних підходах щодо прогнозування, які публікуються в спеціальній економічній літературі. Проаналізуймо деякі результати прогнозування податкових надходжень, ухвалених на їх підставі планів надходжень, а також ступені їх виконання. Окрім того, розглянемо динаміку реальних податкових надходжень, тобто надходжень, приведених до реальних величин з урахуванням індексу цін. Проаналізуймо затверджені в установленому порядку планові показники за основними видами податків: ПДВ (податок на додану вартість), ППГ (прибутковий податок з громадян), ППП (прибутковий податок з підприємств), а також надходження до зведеного бюджету (НЗБ) (табл. 4.2) Таблиця 4.2 Виконання планових надходжень за основними податками
*Діяльність податкової служби України за 1999 рік. — К., 1999. Зазначимо, що податкові надходження становили у зведеному бюджеті у 1997 році 68 %, у 1998 — 75, у 1999 — 76,5 %. Неважко помітити, що обсяги фактичних надходжень до зведеного бюджету істотно відрізняються від планових. Та недовиконання дохідних статей зведеного бюджету не завжди відбувається лише за рахунок недовиконання обсягів податків. Податок на додану вартість у 1997/1998 роках збирався відповідно лише на 89,9 і 82,7 % запланованих обсягів. Якщо використовувати дані Держкомстату щодо динаміки номінального ВВП і дані про реальний ВВП за даними незалежної організації UEPLAG, то можна розрахувати обсяг державного навантаження на економіку як відношення НЗБ до ВВП (табл. 4.3). Таблиця 4.3 Динаміка номінального і реального ВВП
* Тенденції української економіки. Березень 2000 / TACIS. Українсько-європейський консультаційний центр з питань законодавства [UEPLAG], 2000. На перший погляд, обсяг державного навантаження на економіку України в останні роки є відносно невеликим (у 1999 році — 27,5 %). Однак реальну оцінку впливу оподаткування на економіку країни можна одержати, якщо нормувати обсяг державного навантаження на обсяг відносного ВВП, що визначається як відношення ВВП даної країни до середньосвітового. Виникає також питання щодо адекватності оцінок обсягу ВВП до реально існуючого, оскільки офіційна ставка не враховує внеску «тіньового» сектору економіки. В урядовій програмі «Україна 2010 року» припускається, що з урахуванням «тіньового» сектору економіки ВВП у розрахунку на душу населення становив 2000 дол. США на кінець 1999 року, і ця цифра береться як початкова база зростання економіки України на найближче десятиліття. Однак кількісні оцінки «тіньового» сектору економіки України, обчислені за допомогою економетричної моделі рівноваги попиту і пропозиції на грошову масу, не підтвердили цю гіпотезу. З’ясувалося, що обсяг реального ВВП на душу населення в Україні перебуває в проміжку 800—1200 дол. США. Як наслідок нераціонального податкового навантаження маємо, що обсяг надходжень характеризується їхнім суттєвим зниженням у реальних цінах за досліджуваний проміжок часу (табл. 4.4). Таблиця 4.4 Номінальні і реальні податкові надходження,
* Бюлетень НБУ України. — 2000. — № 1. Як відомо, прогнози поділяють: на оперативні — до одного місяця; короткострокові — до одного року; середньострокові — до п’яти років і довгострокові — понад п’ять років. Здійснення та використання прогнозів з різними часовими горизонтами визначається природою прогнозованих процесів. В умовах нестійкого характеру економічних процесів на практиці, по суті, можуть бути реалізовані лише два види прогнозів — оперативний і короткотерміновий. У прогнозуванні податкових надходжень, на нашу думку[2], необхідно брати до уваги, зокрема, фактичні динамічні ряди надходжень податків за попередні періоди. Треба також мати на увазі, що показники за минулі періоди потрібно в багатьох випадках коригувати, що потребує вивчення конкретних економічних особливостей даного періоду з урахуванням величини ставок оподаткування, зміни податкової бази тощо. Відомо, що прогнозування будь-якого економічного показника пов’язане з похибкою прогнозу, величина якої визначає ступінь ризику планів (рішень), які ґрунтуються на прогнозованих економічних показниках. Розгляньмо категорію податкового ризику як одну зі складових багатофакторної оцінки надійності прийняття рішень щодо обсягів планових податкових надходжень на базі їхніх прогнозованих обсягів. Кількісна оцінка міри економічного ризику (зокрема ризику податкових надходжень) є багатовимірною величиною — вектором G = (q 1, …, qn), компоненти якого формуються залежно від мети дослідження, узятої системи гіпотез, суб’єктивного чинника, котрий характеризує ставлення суб’єкта ризику до невизначеності, конфліктності тощо. Одна група компонент цього вектора характеризує ризик як об’єктивну економічну категорію, решту — які враховують ставлення до ризику суб’єкта прийняття рішень — доречно розглядати як суб’єктивні складові міри ризику. У статистичному моделюванні та прогнозуванні вводяться та аналізуються такі поняття, як середній та емпіричний ризики. За показник ступеня середнього ризику зазвичай обирається математичне сподівання квадрата різниці між розрахунковими і фа- На підставі прогнозованих обсягів податкових надходжень визначають планові обсяги, котрі, взагалі кажучи, припускаються дещо меншими, ніж середнє значення прогнозованого обсягу. Отже, крім об’єктивної складової, треба також увести суб’єктивну складову міри ризику, за яку доречно, на наш погляд, обрати ймовірність недовиконання запланованого обсягу податкових надходжень, обчисленого на базі їхнього прогнозованого обсягу. Очевидно, що ступінь ризику (імовірності) недовиконання планового обсягу податкових надходжень повинен бути якомога меншим. Відсоток недовиконання планових податкових надходжень у свою чергу може розглядатися як ще один із показників суб’єктивної оцінки міри ризику. Він задається нормативно залежно від ставлення суб’єкта прийняття рішень до ризику та до обсягів прогнозованих величин, котрі задаються певним інтервалом значень (інтервальний прогноз). Доречно також увести до розгляду як одну з компонент векторної оцінки міри ризику показник ризику невикористаних можливостей, котрий характеризує міру відхилення запланованого обсягу податкових надходжень від максимально можливого прогнозованого обсягу надходжень, здійсненого на підставі використання адекватних математичних моделей. Наголосимо, що всі ці складові міри податкового ризику необхідно використовувати комплексно, системно. Порядок моделі ARIMA задається трьома параметрами: порядок авторегресії р; порядок оператора різниці d для приведення процесу до стаціонарного вигляду; порядок моделі ковзного середнього q. Модель ARIMA (якщо d = 0) запишеться у вигляді:
де yt — величина досліджуваного процесу на час t (t = 1, 2,... T); q1, q2, …, q q — коефіцієнти моделі ковзного середнього; Ф1, Ф2, Ф p — авторегресійні коефіцієнти; d — параметр, що визначає середнє значення; Т — кількість періодів спостережень; Іншими словами, модель ARIMA ґрунтується на прогнозуванні значення відповідного економічного показника на час t на підставі значень, які спостерігалися у попередні періоди. Кількість необхідних попередніх спостережень визначається порядком авторегресії. Крім того, використовують похибки, одержані в процесі прогнозування попередніх значень. Кількість цих похибок визначається порядком моделі ковзного середнього. Авторегресійна складова і модель ковзного середнього утворюють модель ARMA, яку можна використати для прогнозування стаціонарного випадкового процесу, тобто процесу, де математичне сподівання, дисперсія та моменти вищих порядків не залежать від часу. На жаль, у більшості часових рядів економічних показників випадки існування стаціонарних випадкових процесів трапляються рідко. Для приведення процесу до стаціонарного вигляду, як правило, використовується оператор різниці, і, відповідно, модель ARMA перетворюється в модель ARIMA. Ще одна особливість, яка проявилася у результаті аналізу статистичних характеристик рядів податкових надходжень, — це відсутність значущого зв’язку між надходженнями в сусідні місяці. Якщо побудувати авторегресійну функцію надходжень за окремими типами податків, то виявиться, що зв’язок між суміжними у часі значеннями відносно незначний (дискретність рядів дорівнює одному місяцю). Здебільшого автокореляційна функція має екстремум, якщо значення величини лага — 12 місяців. З року в рік у певні місяці надходження перевищують середній рівень, а в інших — навпаки. Це вказує на існування циклічності, період якої дорівнює 1 року (12 місяцям). Наприклад, найкращим чином обсяг надходження на січень наступного року можна визначити, якщо відомі надходження за січень попередніх років. Цю особливість процесу добре описує модель ARIMAS m, n, l, де параметри m, n, l мають зміст, аналогічний параметрам p, d, q моделі ARIMA зі зрушеннями на 12 кроків. Перший етап побудови моделі ARIMA*ARIMAS полягає в тому, що за видом авторегресійної функції, яка включає в себе дані про характер тренду, наявність циклічності, порядок авторегресійного і ковзного середнього, здійснюється вибір параметрів моделі. Вибір моделі може здійснюватися на підставі зниження показника ризику згідно з обраною моделлю на базисному інтервалі. За використання моделі ARIMA розраховуються такі похибки: 1. MSE — середній квадрат похибки:
де х (і) — фактичні значення показника в і- му періоді; i = 1, …, T, 2. MAE — середня абсолютна похибка:
3. MPD — середня відсоткова похибка:
4. MAPE — середня абсолютна відсоткова похибка:
Окрім того, під час побудови моделі враховуються похибки оцінок коефіцієнтів моделі Ф і q, тобто модель вважається адекватною, якщо всі її параметри будуть значущими на 95 % рівня довіри (чи 5 % ступеня ризику). На основі даної методики були проаналізовані ряди податкових надходжень по окремих районах м. Києва на підставі щомісячних даних з 1996 до 1999 року (за винятком грудня 1999 року), тобто Т = 47. Були також отримані прогнозовані щомісячні значення на 2000 рік по Києву. Надходження по м. Києву загалом з метою зниження похибки прогнозу визначались як сума прогнозів податкових надходжень по окремих районах. Для районів, де критерій мінімуму похибки конфліктував з критерієм значущості відповідних коефіцієнтів, було знайдено два варіанти прогнозів — песимістичний та оптимістичний, що дозволило по м. Києву загалом одержати два прогнозних значення — 5,17 млрд грн (песимістичний прогноз) і 5,4 млрд грн (оптимістичний прогноз). Отримані також обсяги фактичних податкових надходжень за перших три місяці 2000 року, котрі становлять 1,264 млрд грн. Прогнозований обсяг згідно з оптимістичним варіантом дорівнює 1,285 млрд грн. А згідно з песимістичним — 1,245 млрд грн. Іншими словами, оптимістичний варіант прогнозу перевищує фактичну величину на 1,7 %, а песимістичний виявився меншим за фактичний на 1,5 %, що свідчить про достовірність прогнозу. Що стосується достовірності прогнозу на друге півріччя 2000 року, то на основі існування взаємозв’язку щодо темпів зростання грошової маси, темпів інфляції можна зробити припущення, що оптимістичний варіант прогнозу в номінальних цінах буде також дещо перевищений, хоча тенденція зменшення реальних надходжень скоріше всього збережеться. Розгляньмо постановку задачі розрахунку похибки прогнозу. Доцільно обчислити ступінь ризику, що пов’язаний з моделлю прогнозування податкових надходжень по Києву, як один зі складових векторної оцінки міри податкового ризику за умови, що прогнозована величина розраховується як сума прогнозованих обсягів надходжень по окремих районах. Нехай прогнозована величина обсягів податкових надходжень по Києву загалом
тобто
де l — горизонт прогнозу, Дисперсія загальної суми прогнозованих надходжень по м. Києву дорівнює:
Оскільки похибки прогнозування на базі моделі ARIMA являють собою «білий шум» (мають нормальний закон розподілу), то коефіцієнти кореляції цих похибок дорівнюють нулю ( У нашому випадку коваріаційна матриця набуває діагонального вигляду, а дисперсія та середньоквадратичне відхилення (похибка) прогнозу дорівнює:
Як величину дисперсії прогнозу можна використати величину MSE, помножену на коефіцієнт С:
У нашому випадку маємо такі дані: T = 47, p + q + m + l = 8, звідси Визначимо як одну з компонент вектора податкового ризику ймовірність можливого недовиконання планових податкових надходжень. Ризик 10 %-го недовиконання планового показника за прогнозування на один крок дорівнюватиме:
де V — аналог коефіцієнта варіації:
s — похибка прогнозу, отримана на базовому інтервалі; xp — прогнозоване значення податкових надходжень; Ф(х) — функція Лапласа. Розрахуємо величину ризику щомісячних сумарних надходжень для однокрокового прогнозу. Прогнозована величина щомісячних надходжень для м. Києва загалом на 2000 рік xp = 430 млн грн. Обчислимо величини s та V відповідно до виразів (4.75) та (4.76) (s = 12,3 млн грн; V =
Для одного з районів Києва середня прогнозована величина щомісячних надходжень на 2000 рік дорівнює 63,2 млн грн, а величина похибки прогнозу становить відповідно 3,9 млн грн. V = 3,9/63,2 = 0,0625. Відповідно значення однієї із суб’єктивних компонент вектора міри податкового ризику (ймовірне недовиконання надходжень) дорівнює:
Наведені розрахунки свідчать, зокрема, про те, що коли б прогноз здійснювався за сумарним масивом надходжень у попередні роки, то похибка на базовому інтервалі була б такою: s2 =
Цей ефект пояснюється тим, що випадкові (не систематичні) похибки прогнозів по окремих районах взаємно компенсуються, чого не відбувається у використанні для прогнозування показників по місту загалом (за інтервалами). Звідси можна зробити висновок про доцільність поділу прогнозування загальної суми податкових надходжень на порайонні складові. Обчислимо ступінь ризику на 1 %-му рівні можливого невиконання середнього прогнозованого обсягу податкових надходжень по м. Києву загалом:
Як бачимо, ступінь податкового ризику недовиконання прогнозованих податкових надходжень на 1 %-му рівні залишився значним. Тому, на нашу думку, є сенс установити планове значення надходжень дещо меншим від прогнозованого: x пл = kxp, де x пл — плановий обсяг податкових надходжень, k — коригуючий коефіцієнт (відношення обсягів планових надходжень до прогнозованих). Розгляньмо ризик недовиконання планових податкових надходжень на 10 %-му рівні (k = 0,9):
Ризик на рівні 1 %-го недовиконання планових надходжень у цьому випадку також значно зменшився:
Практичну користь також має обернена задача: на якому рівні (меншому від середньопрогнозованого) потрібно встановити планові надходження, щоб зменшити ризик 10 %-го недоотримання запланованих обсягів податкових надходжень, наприклад, до ступеня p = 0,0001. Припустимо, що:
Звідси отримаємо:
Оскільки величина планових надходжень x пл = kxp, то з виразу
отримаємо:
Отже, щоб зменшити ризик 10 %-го невиконання планових надходжень до 0,0001, потрібно встановити плановий обсяг надходжень на 1 %-му рівні нижчим за їхній середній прогнозований обсяг. Запропонований підхід дозволяє за відомою (заданою) величиною компоненти векторної оцінки міри ризику (імовірності недовиконання надходжень) розрахувати величину планових надходжень як частку від їхнього прогнозованого обсягу. Усі наведені міркування стосуються компоненти векторної оцінки міри ризику прогнозу на один крок. Відомо, що за збільшення прогнозного інтервалу похибка прогнозу також збільшується. Знайдемо похибку в прогнозуванні податкових надходжень на один рік (12 кроків). Дисперсія похибки прогнозування на l кроків визначається як:
де Оскільки коефіцієнти y l невідомі, то похибка на річному інтервалі розраховується за їх максимально можливих значень, які за умовою стаціонарності процесу не перевищують 1, тобто:
Відповідне значення величини Розрахуємо величину податкового ризику недовиконання планових надходжень у прогнозуванні на один рік та його зниження введенням коригуючого коефіцієнта (табл. 4.5). Таблиця 4.5 Ступінь ризику (ймовірність) недовиконання
Нехай
де х' — величина недовиконання планових показників у відсотках. У формулі для розрахунків імовірності недовиконання обсягу планових податкових надходжень використовуються таблиці розподілу Лапласа:
Як випливає з розрахунків (див. табл. 4.5), 10 %-ве недовиконання прогнозу, отриманого за допомогою моделі ARIMA по м. Києву, трапляється рідко. Наголосимо, що навіть 1 %-ве недовиконання (як ступінь ризику) становить значну величину (50 млн грн). Звідси як нормативний, на наш погляд, краще ввести ступінь ризику 1 %-го недовиконання планових надходжень. Відповідно отримаємо такі значення ймовірності недовиконання залежно від коефіцієнта k: P (1,00) = 0,326; P (0,995) = 0,252; P (0,99) = 0,184; Як бачимо з наведених розрахунків, використання коригуючого коефіцієнта k дозволяє зменшити ризик як імовірність 1 %-го недовиконання планових надходжень установленням планового обсягу податкових надходжень як частки від їхнього середнього прогнозованого обсягу. Треба пам’ятати, що запропонована методика вказує лише на необхідність зниження планових обсягів надходжень щодо прогнозованих. Але за цих умов виникає ризик невикористаних можливостей, оскільки у такому підході і обсяг надходжень, і видаткова частина бюджету будь-якого рівня ієрархії управління буде (під час планування) скорочена. Тому пропонується також більш загальний підхід до визначення планових обсягів податкових надходжень. Якщо розглядати, як про це вже йшлося вище, ще одну компоненту векторної оцінки міри ризику, а саме — показник ступеня ризику невикористаних можливостей, то, на наш погляд, доречно ввести до розгляду інтегрований (комплексний) показник ступеня ризику як міру відхилення від цілей для знаходження планового обсягу податкових надходжень на підставі їхнього прогнозованого обсягу. За визначеного на етапі прогнозування, середнього прогнозованого обсягу надходжень xp та отриманої оптимістичної (максимальної) оцінки обсягу надходжень
де R (k, l) — інтегрований показник ступеня ризику; Величина l(0 £ l £ 1) визначається залежно від пріоритетів, які вказують на те, що важливіше з погляду людей, котрі приймають відповідні рішення, не допустити недовиконання планових надходжень чи не запланувати надмірно низький бюджет.
|


 — «білий шум».
— «білий шум».
 — прогнозовані значення цього показника в і -му періоді;
— прогнозовані значення цього показника в і -му періоді;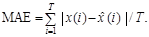


 дорівнює сумі прогнозних значень надходжень:
дорівнює сумі прогнозних значень надходжень:

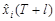 — обсяг податкових надходжень по і -му району м. Києва, (n – 1) — кількість міських районів i = 1, …, n – 1, (n – 1) = 14;
— обсяг податкових надходжень по і -му району м. Києва, (n – 1) — кількість міських районів i = 1, …, n – 1, (n – 1) = 14;  — надходження від загальноміських комунальних служб; n — індекс, яким позначаються загальноміські комунальні служби (n = 15). Кожна з прогнозованих величин містить у собі похибку прогнозу, яка визначається похибкою на базовому інтервалі.
— надходження від загальноміських комунальних служб; n — індекс, яким позначаються загальноміські комунальні служби (n = 15). Кожна з прогнозованих величин містить у собі похибку прогнозу, яка визначається похибкою на базовому інтервалі.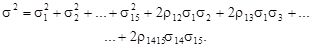 (4.74)
(4.74) ) супроти коефіцієнтів кореляції похибок статистичних даних, у яких існував прямий взаємозв’язок між надходженнями у кожному з районів, що значною мірою визначалося впливом макроекономічних показників, загальних для всіх районів.
) супроти коефіцієнтів кореляції похибок статистичних даних, у яких існував прямий взаємозв’язок між надходженнями у кожному з районів, що значною мірою визначалося впливом макроекономічних показників, загальних для всіх районів. (4.75)
(4.75)

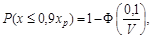
 (4.76)
(4.76)









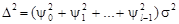 ,
, — похибка прогнозу на базовому інтервалі;
— похибка прогнозу на базовому інтервалі;  — коефіцієнти подання моделі ARIMA як процесу ковзного се-
— коефіцієнти подання моделі ARIMA як процесу ковзного се-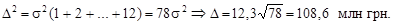
 за прогнозного значення надходжень по Києву на 2000 рік
за прогнозного значення надходжень по Києву на 2000 рік  млн грн дорівнює
млн грн дорівнює 


 інтегрований показник ступеня ризику будується, зокрема, так:
інтегрований показник ступеня ризику будується, зокрема, так:
 — показник ступеня ризику невикористаних можливостей; R 2(kxp) — показник ступеня ризику як імовірність недовиконання планових надходжень. Зазначимо, що коефіцієнт k > 0 не обов’язково повинен бути меншим за одиницю.
— показник ступеня ризику невикористаних можливостей; R 2(kxp) — показник ступеня ризику як імовірність недовиконання планових надходжень. Зазначимо, що коефіцієнт k > 0 не обов’язково повинен бути меншим за одиницю.


