Організація рекламної кампанії
А. Провести аналіз власного ризику проекту (100 імітацій) на підставі використання генератора випадкових чисел. Б. Здійснити статистичний аналіз взаємозалежності між ключовими змінними. В. Перевірити гіпотезу щодо нормального закону розподілу вихідних даних і отриманих результатів. 4. Розв’язати попередній приклад, припустивши гіпотезу щодо дискретного розподілу значень ключових змінних. 5. Час, упродовж якого інспектор податкової служби перевіряє квартальний звіт (t), є випадковою величиною, розподіленою відповідно до закону Вейбула. Середній час, що витрачається на перевірку, дорівнює 6. Періодичність перевірки підприємств податковою інспекцією — випадкова величина (Δ t), яка має закон гама-розподілу. Середній інтервал перевірки становить 7. Використовуючи умови попередньої задачі, визначити кількість перевірок податковою інспекцією за перший рік роботи підприємства.
[1] Моисеев Н. Н. Математические задачи системного анализа. — М.: Наука. Глав. ред. физ.-мат. лит., 1981. [2] Варфоломеев В. И. Алгоритмическое моделирование элементов экономических систем: Практикум: Учеб. пособие. — М.: Финансы и статистика, 2000. [3] Петров А. А. Экономика. Модели. Вычислительный эксперимент. — М.: Наука, 1996. Організація рекламної кампанії Нехай деяка фірма (підприємство, установа) починає рекламувати новий товар чи послугу. Ясно, що прибуток від майбутнього продажу повинен перекривати витрати на цю кампанію. Ясно також, що спочатку витрати можуть перевищувати прибуток, бо лише невелика частка потенційних покупців буде інформована щодо новинки. Згодом, у міру збільшення обсягів продажу, можна вже розраховувати на помітний прибуток, і, врешті, настане момент, коли ринок насититься, і надалі рекламувати товар не буде сенсу. Модель рекламної кампанії ґрунтується на таких основних гіпотезах. Розглядається величина dN/dt — швидкість зміни в часі кількості споживачів, котрі дізналися про товар і мають намір і кошти купити його (t — час, що минув з початку рекламної кампанії), N (t) — кількість уже поінформованих клієнтів. Вважається, що dN/dt пропорційна кількості покупців, які ще не знають про цей товар (послуги), тобто величині a1(t) (N 0 – N (t)), де N 0 — загальна кількість потенційних платоспроможних покупців, a1(t) > 0 характеризує інтенсивність рекламної кампанії (що фактично визначається витратами на рекламу в даний момент часу). Припускається також, що ті, хто дізнався про товар, так чи інакше поширюють отриману інформацію серед необізнаних, виступаючи в ролі додаткових рекламних «агентів» фірми. Їхній внесок дорівнює величині a2(t)(N (t)(N 0 – N (t))). Він буде тим більшим, чим більша кількість агентів. Величина a2(t) > 0 характеризує ступінь спілкування покупців між собою (вона може бути встановлена опитуванням). У результаті отримаємо рівняння
Якщо a1(t) >> a2(t) N (t), то з (4.1) отримаємо модель типу моделі Мальтуса (див. розд. 2, п. 16), якщо ж a1(t) << a2(t) N (t), — рівняння логістичної кривої (див. розд. 2, п. 18). Аналогія є цілком зрозумілою, бо в побудові даної моделі та моделі зростання чисельності популяції використовувалася та сама ідея «насичення»: швидкість зростання в часі деякої величини пропорційна добутку поточного значення цієї величини N (t) на різницю ((N 0 – N (t)) між її рівноважним (популяція) чи граничним (покупці) й поточним значеннями. Аналогія між обома процесами закінчується, якщо в деякий момент часу величина стає нульовою чи навіть від’ємною (для цього необхідно, щоб один чи обидва коефіцієнти a1(t), a2 стали від’ємними). Подібний негативний ефект досить часто зустрічається в рекламних кампаніях і повинен націлювати їх організаторів на те, щоб чи змінити характер реклами, чи зовсім відмовитися від неї. Заходи з метою збільшення популярності товару можуть залежно від значень величин спрямовуватися на поліпшення результатів як прямої, так і опосередкованої реклами. Модель (4.1) не має розв’язків, що дорівнюють нулеві в кінцевий момент часу. Якщо розглянути модель (4.1) в околі точки N (t = 0) = N (0) = 0 (t = 0 — момент початку рекламної кампанії), вважаючи, що N << N 0, a2(t) N << a1(t), то рівняння (4.1) набере вигляду:
а його розв’язок —
що задовольняє, природно, початкову умову, якщо t = 0. З (4.2) відносно легко вивести співвідношення між рекламними витратами та прибутком з початку рекламної кампанії. Позначимо через р величину прибутку від одиничного продажу, якою б вона була без витрат на рекламу. Припустимо для спрощення, що кожен покупець купує лише одну одиницю товару. Коефіцієнт a1(t) за своїм змістом означає кількість рівнозначних рекламних дій в одиницю часу (наприклад, розміщення однакових афіш). Через s позначимо вартість (ціну) елементарного акту реклами. Тоді сумарний прибуток дорівнюватиме:
а витрати —
Прибуток перевищує витрати на рекламу за умови pN 0 > s, і коли реклама є дієвою й недорогою, а ринок досить місткий, то виграш досягається з перших же кроків кампанії (в дійсності між оплатою реклами, рекламною дією й наступною купівлею має місце лаг — затримка в часі, котра може бути врахована лише в більш деталізованих моделях). У випадку не дуже ефективної чи дорогої реклами фірма із самого початку несе збитки. Але це не привід, щоб відмовитися від реклами. Справді, вираз (4.3) та отримана на його підставі умова pN 0 > s справедливі лише за малих значень N (t), коли функції P та S зростають у часі за однаковими законами. Зі збільшенням N (t) відкинуті в (4.1) складові стають помітними, зокрема, посилюється дія опосередкованої реклами. Тому функція N (t) може стати «швидшою» функцією часу, ніж у формулі (4.3). Цей нелінійний ефект у зміні величини N (t) за незмінного темпу зростання витрат дає можливість від- Пояснимо це твердження на частковому випадку рівняння (4.1) з постійними коефіцієнтами a1, a2. Виконаємо заміну змінних:
Тоді (4.1) зводиться до логістичного рівняння
яке має розв’язок
Тут З (4.4) видно, що похідна функції
У цей період поточного, тобто отримуваного в одиницю часу прибутку, маємо:
Віднімаючи від
отримаємо:
тобто різниця між початковим і максимальним поточним прибутками може бути досить значною. Сумарний (інтегральний) економічний ефект від кампанії (його необхідною умовою є, очевидно, виконання нерівності Як випливає з (4.4), починаючи з деякого моменту рекламування стає невигідним. Дійсно, коли
Його розв’язок прямує до граничного значення Аналогічні характеристики обчислюються для рівняння (4.1) та різних його узагальнень, що широко використовуються також для опису впровадження технологічних та інших новацій. Наведений вище аналіз стосується низки актуальних задач мікроекономічного рівня.
|

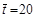 хв. Коефіцієнт варіації величини t дорівнює CVt = 0,52. Необхідно змоделювати для заданих умов випадкове число t (кількість прогонів дорівнює 10).
хв. Коефіцієнт варіації величини t дорівнює CVt = 0,52. Необхідно змоделювати для заданих умов випадкове число t (кількість прогонів дорівнює 10).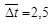 місяця. Коефіцієнт варіації величини Δ t дорівнює CV = 0,38. Треба змоделювати для заданих умов можливі моменти перевірок підприємства податковою інспекцією (число прогонів узяти рівним 10).
місяця. Коефіцієнт варіації величини Δ t дорівнює CV = 0,38. Треба змоделювати для заданих умов можливі моменти перевірок підприємства податковою інспекцією (число прогонів узяти рівним 10).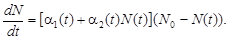 (4.1)
(4.1)
 (4.2)
(4.2) (4.3)
(4.3)

 (4.4)
(4.4) (4.5)
(4.5) , отже, N (0) = 0, і початкова умова виконується.
, отже, N (0) = 0, і початкова умова виконується.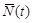 і, отже, функція N (t) за умови t > 0 може бути більшою, ніж її початкове значення (за умови, що
і, отже, функція N (t) за умови t > 0 може бути більшою, ніж її початкове значення (за умови, що  чи
чи  ). Максимум похідної по
). Максимум похідної по  досягається, коли
досягається, коли 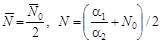 :
:

 початковий поточний прибуток
початковий поточний прибуток ,
,
 ), визначається всім її перебігом, характеристики котрого обчислюються з (4.4), (4.5) за допомогою квадратури (інтегрування).
), визначається всім її перебігом, характеристики котрого обчислюються з (4.4), (4.5) за допомогою квадратури (інтегрування). , рівняння (4.4) можна записати у вигляді:
, рівняння (4.4) можна записати у вигляді: (4.6)
(4.6) за умови t ® 0 (а функція N (t)® N 0) згідно з повільним експоненційним законом. В одиницю часу з’являється надто мала кількість нових покупців, і одержуваний прибуток за будь-яких умов не може перекрити додаткових витрат.
за умови t ® 0 (а функція N (t)® N 0) згідно з повільним експоненційним законом. В одиницю часу з’являється надто мала кількість нових покупців, і одержуваний прибуток за будь-яких умов не може перекрити додаткових витрат.


