Затухающие и вынужденные колебаниях. Резонанс.
Силы, действующие между телами внутри рассматриваемой системы тел, называют внутренними силами. Силы, действующие на тела системы со стороны других тел, не входящих в эту систему, называют внешними силами. Свободными колебаниями называют колебания, возникающие под действием внутренних сил. Затуханием колебаний называется постепенное уменьшения амплитуды колебаний с течением времени, обусловленное потерей энергии колебательной системой. Затухание свободных колебаний механической системы обусловлено диссипацией (рассеянием или потерей) ее энергии в следствие действия на систему непотенциальных сил сопротивления(трения). Затухающие колебания описываются функцией
b - коэффициент затухания, Логарифмическим декрементом затухания q называется натуральный логарифм отношения амплитуд колебаний в моменты времени t и t+T
Логарифмический декремент затухания – величина, обратная числу колебаний N, по истечении которых амплитуда уменьшается в e раз Колебания, возникающие под действием внешних периодически изменяющихся сил, называются вынужденными колебаниями. Резкое увеличение амплитуды вынужденных при приближении (совпадении) частоты вынужденных колебаний к частоте свободных колебаний системы называют резонансом.
|
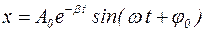
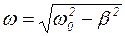- собственная циклическая частота колебаний диссипативной системы, w0 – циклическая частота свободных колебаний системы в отсутствие трения, 
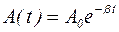- амплитуда затухающих колебаний.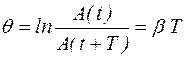
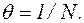Промежуток времени t, необходимый для этого, называется временем релаксации 
.
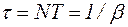