Тавровые сечения. Пример 6. Дано: сечение размерами = 1500 мм, = 50 мм, b = 200 мм, h = 400 мм; а = 80 мм; бетон класса В25 (Rb = 14,5 МПа)
Пример 6. Дано: сечение размерами Требуется определить площадь сечения продольной арматуры. Расчет. h 0 = 400 - 80 = 320 мм. Расчет производим согласно п. 3.25 в предположении, что сжатая арматура по расчету не требуется. Проверим условие (3.32), принимая Rb т.е. граница сжатой зоны проходит в полке, и расчет производим как для прямоугольного сечения шириной b = Вычисляем значение
т.е. сжатая арматура действительно по расчету не требуется. Площадь сечения растянутой арматуры вычисляем по формуле (3.23)
Принимаем 4Æ28(Аs = 2463 мм2). Пример 7. Дано: сечение размерами Требуется определить площадь сечения растянутой арматуры. Расчет. h 0= 600 - 65 = 535 мм. Расчет производим согласно п. 3.25 в предположении, что сжатая арматура по расчету не требуется. Так как Rb граница сжатой зоны проходит в ребре и площадь сечения растянутой арматуры определим по формуле (3.33), принимая площадь сечения свесов равной Аov = (
Принимаем 4Æ25(Аs = 1964 мм2), Пример 8. Дано: сечение размерами Требуется проверить прочность сечения. Расчет. h 0= 600 - 70 = 530 мм. Проверку прочности производим согласно п. 3.23, принимая Для этого по формуле (3.29) определим высоту сжатой зоны, приняв площадь свесов равной Аov = (
Rbbx (h 0 - 0,5 х) + RbAov (h 0 -0,5 Расчет наклонных сечений на действие поперечных сил Пример 9. Дано: ребро ТТ-образной плиты перекрытия с размерами сечения: h = 350 мм, b = 85 мм; а = 35 мм; бетон класса В15 (Rb - 8,5 МПа, Rbt = 0,75 МПа); ребро армировано плоским каркасом с поперечными стержнями из арматуры класса А400 (Rsw = 285 МПа) диаметром 8 мм (Аsw = 50,3 мм2) шагом sw = 100 мм; полная равномерно распределенная нагрузка, действующая на ребро, q = 21,9 кН/м; временная эквивалентная нагрузка qv = 18 кН/м; поперечная сила на опоре Qmax = 62 кН. Требуется проверить прочность наклонных сечений и бетонной полосы между наклонными сечениями.
Расчет. h 0= h - а = 350 - 35 = 315 мм. Прочность бетонной полосы проверим из условия (3.43): 0,3 Rbbh 0 = 0,3×8,5×85×315 = 68276 Н > Q max = 62 кН, т.е. прочность полосы обеспечена. Прочность наклонного сечения по поперечной силе проверим согласно п. 3.31. По формуле (3.48) определим интенсивность хомутов
Поскольку
Согласно п. 3.32 определим длину проекции невыгоднейшего наклонного сечения с. q 1 = q – qv /2= 21,9 - 18/2 = 12,9 кН/м (Н/мм). Поскольку
Принимаем с 0 = с = 280,7 мм. Тогда Qsw = 0,75 qswc 0= 0,75×143,3×280,7 = 30168 Н = 30,17 кН.
Q = Q max – q 1 c = 62 –12,9×0,28 = 58,4 кН. Проверяем условие (3.44) Qb + Qsw = 33,8 + 30,17 = 63,97 Н > Q = 58,4 кН, т.е. прочность наклонных сечений обеспечена. Проверим требование п. 3.35:
т.е. требование выполнено. Условия п. 5.21 sw < h 0/2 = 315/2 = 157 мм и sw < 300 мм также выполнены. Пример 10. Дано: свободно опертая балка перекрытия с размерами сечения: b - 200 мм, h - 400 мм; h 0 - 370 мм; бетон класса В25 (Rbt -1,05 МПа); хомуты двухветвевые диаметром 8 мм (Аsw = 101 мм2) с шагом sw = 150 мм; арматура класса А240 (Rsw = 170 МПа); временная эквивалентная по моменту нагрузка qv = 36 кН/м, постоянная нагрузка qg = 14 кН/м; поперечная сила на опоре Q max= 137,5 кН. Требуется проверить прочность наклонных сечении. Расчет. Прочность наклонных сечений проверяем согласно п. 3.31. По формуле (3.48) определим интенсивность хомутов
Поскольку
Согласно п. 3.32 определяем длину проекции невыгоднейшего наклонного сечения: q 1= qg + 0,5 qv = 14 + 0,5×36 = 32 кН/м (Н/мм). Поскольку
значение с принимаем равным 1161 мм > 2 h 0 = 740 мм. Тогда с 0= 2 h 0 = 740 мм и Qsw = 0,75×114,5×740 = 63548 Н = 63,55 кН;
Q = Q max – q 1 c = 137,5 - 32×1,161 = 100,35 кН. Проверяем условие (3.44) Qb + Qsw = 37,14 + 63,55 =100,69 кН > Q = 100,35 кН. т.е. прочность наклонных сечений обеспечена. Пример 11. Дано: свободно опертая балка перекрытия пролетом l = 5,5 м; полная равномерно распределенная нагрузка на балку q = 50 кН/м; временная эквивалентная нагрузка qv =36 кН/м; размеры поперечного сечения b = 200 мм, h = 400 мм; h 0= 370 мм; бетон класса В15 (Rbt = 0,75 МПа); хомуты из арматуры класса А240 (Rsw = 170 МПа). Требуется определить диаметр и шаг хомутов у опоры, а также выяснить, на каком расстоянии и как может быть увеличен шаг хомутов. Расчет. Наибольшая поперечная сила в опорном сечении равна
Определим требуемую интенсивность хомутов приопорного участка согласно п. 3.33, б По формуле (3.46) определяем Мb
Согласно п. 3.32 q 1= q - 0,5 qv = 50 – 0,5×36 = 32 кН/м (Н/мм).
Так как 2 Mb / h 0 - Q max = 2×30,8×106/370 - 137500 = 28986 Н < Qbl = 62790 Н, интенсивность хомутов определяем по формуле (3.52)
Согласно п. 5.21 шаг хомутов sw у опоры должен быть не более h 0/2= 185 и 300 мм, а в пролете – 0,75 h 0 = 278 и 500 мм. Максимально допустимый шаг у опоры согласно п. 3.35 равен
Принимаем шаг хомутов у опоры sw 1 = 150 мм, а в пролете 250 мм. Отсюда Asw = Принимаем в поперечном сечении два хомута по 10 мм (Asw = 157мм2). Таким образом, принятая интенсивность хомутов у опоры и в пролете соответственно равны:
Проверим условие (3.49): 0,25× Rbtb = 0,25×0,75×200 = 37,5 Н/мм < qws 1, и 37,5 < qsw 2. Следовательно, значения qsw 1и qsw 2не корректируем. Определим, согласно п. 3.34 длину участка l 1; с интенсивностью хомутов qsw 1. Так как D qsw = 0,75(177,9 – 106,7) = 53,4 Н/мм > q 1 = 32 Н/мм, значение l 1 вычислим по формуле (3.59), приняв Qb, min= 0,5 Rbtbh 0 = 0,5×55500 = 27750 Н.
Принимаем длину участка с шагом хомутов sw 1 - 150 мм равной 0,9 м.
|

 = 1500 мм,
= 1500 мм, 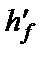 = 50 мм, b = 200 мм, h = 400 мм; а = 80 мм; бетон класса В25 (Rb = 14,5 МПа), арматура класса А400 (Rs = 355 МПа); изгибающий момент М = 260 кН/м.
= 50 мм, b = 200 мм, h = 400 мм; а = 80 мм; бетон класса В25 (Rb = 14,5 МПа), арматура класса А400 (Rs = 355 МПа); изгибающий момент М = 260 кН/м. = 0:
= 0: < a R = 0,39 (см. табл. 3.2),
< a R = 0,39 (см. табл. 3.2), = 14,5×1500×320(1 -
= 14,5×1500×320(1 -  )/355 = 2446 мм2.
)/355 = 2446 мм2. = 0,356 < a R = 0,39 (см. табл. 3.2), следовательно, сжатая арматура не требуется.
= 0,356 < a R = 0,39 (см. табл. 3.2), следовательно, сжатая арматура не требуется.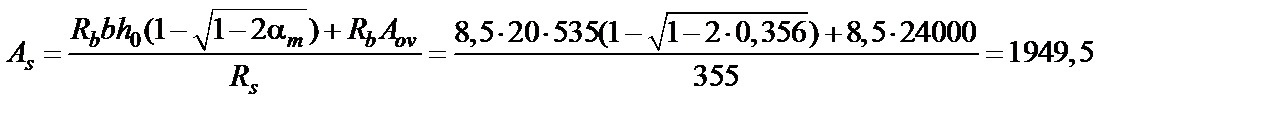 мм2.
мм2. = 355×1964 = 697220 Н > Rb
= 355×1964 = 697220 Н > Rb  мм < x Rh 0 = 0,531×530 = 281 мм (где x R найдено из табл. 3.2).
мм < x Rh 0 = 0,531×530 = 281 мм (где x R найдено из табл. 3.2).
 Н/мм.
Н/мм. =
=  = 2,25 >0,25, т.е. условие (3.49) выполнено, хомуты полностью учитываем и значение Мb определяем по формуле (3.46)
= 2,25 >0,25, т.е. условие (3.49) выполнено, хомуты полностью учитываем и значение Мb определяем по формуле (3.46) = 1,5×0,75×85×3152 = 9,488×106 Н/мм.
= 1,5×0,75×85×3152 = 9,488×106 Н/мм. < 2 h 0.
< 2 h 0. H = 33,8 кН.
H = 33,8 кН. = 102 мм > sw = 100 мм,
= 102 мм > sw = 100 мм, Н/мм.
Н/мм. = 0,545 > 0.25, т.е. условие (3.49) выполняется, хомуты учитываем полностью и значение Мb определяем по формуле (3.46)
= 0,545 > 0.25, т.е. условие (3.49) выполняется, хомуты учитываем полностью и значение Мb определяем по формуле (3.46)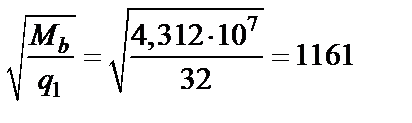 мм >
мм >  = 1017 мм,
= 1017 мм, Н = 37,14 кН;
Н = 37,14 кН; кН.
кН. = 62790 Н.
= 62790 Н. = 161,9 Н/мм.
= 161,9 Н/мм. = 149,3» 150 мм.
= 149,3» 150 мм. = 142,9 мм2.
= 142,9 мм2. Н/мм;
Н/мм;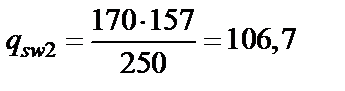 Н/мм.
Н/мм. мм
мм


